El modelo epidemiológico SIR (6)
2020-03-23
El modelo SIR es un modelo muy sencillo del comportamiento de una epidemia a lo largo del tiempo. Tras explicar algunas características del modelo, vimos cómo simplificar el modelo para analizar el comienzo de la propagación de una nueva epidemia, así como el comportamiento de la proporción de infectados en esta fase inicial, cómo relacionar las variables sin necesidad de integrar en el tiempo y cómo calcular el máximo número de infectados simultáneos. Hoy veremos cómo calcular el resultado final de la epidemia.
Recordemos que el modelo sigue a lo largo del tiempo t la evolución de la proporción de susceptibles S(t), la proporción de infectados I(t) y la proporción de recuperados (inmunes y fallecidos) R(t) mediante el siguiente sistema de ecuaciones diferenciales ordinarias:
dS ⁄ dt = −(R0 ⁄ tI) S I;
dI ⁄ dt = (R0 ⁄ tI) S I − (1 ⁄ tI) I;
dR ⁄ dt = (1 ⁄ tI) I.
El parámetro R0 es el número medio de contagios por infectado cuando toda la población es susceptible y el parámetro tI es el tiempo medio que permanece un paciente infectado.
La epidemia acaba tras un tiempo infinito con S(∞) susceptibles no contagiados, R(∞) recuperados o inmunes (es decir, gente que en algún momento pasó por la infección o tenía inmunidad de antemano) y ningún infectado: I(∞) = 0. Esto significa lo siguiente:
S(∞) + R(∞) = 1.
Gracias a las relaciones que calculamos en un artículo previo, podemos escribir la anterior relación en función de una de las variables:
S(0) e−R0 [R(∞)−R(0)] + R(∞) = 1.
Igual que en otras ocasiones, es posible simplificar la expresión en el caso de una epidemia en la que se parte de un número muy pequeño de infectados y el resto de la población inicial es susceptible: S(0) ≅ 1, I(0) ≪ 1, R(0) ≅ 0. La máxima proporción de infectados simultáneos queda de la siguiente forma:
e−R0 R(∞) + R(∞) ≅ 1.
El valor de R(∞) que satisface esta ecuación trascendente es la proporción de la población que en un momento u otro contrae la infección en este escenario simplificado. La siguiente curva ilustra esta solución simplificada:
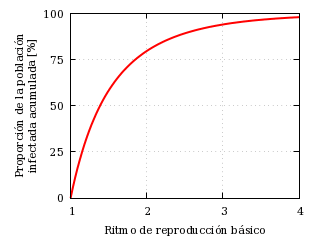
Proporción acumulada de infecciones frente al ritmo reproductivo
básico (R0 en las
ecuaciones).
Cuando no hay inmunidad, basta un ritmo de reproducción moderado para que la mayor parte de la población contraiga la infección. Ahora bien, este modelo elemental no diferencia entre casos que necesitan atención sanitaria y casos leves que pasan desapercibidos.
Categorías: Matemáticas, Salud
Permalink: http://sgcg.es/articulos/2020/03/23/el-modelo-epidemiologico-sir-6/
