Agosto de 2015
Calendario de artículos de de 2015
| lu | ma | mi | ju | vi | sá | do |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 |
Tensiones o esfuerzos mecánicos (10)
2015-08-31
La mecánica de los medios continuos se ocupa del estudio del comportamiento macroscópico de los sólidos y los fluidos no como sistemas de partículas sueltas, sino como medios infinitamente divisibles. Se trata de una disciplina que, además de poder ser interesante por sus propios méritos, es la base de buena parte de nuestro actual desarrollo tecnológico. Uno de los conceptos más importantes de la mecánica de los medios continuos es el del tensor de tensiones o esfuerzos, que es una descripción matemática del estado de fuerzas por unidad de superficie en el seno de un medio continuo. Vimos recientemente que las tensiones en un medio continuo quedan caracterizadas mediante un tensor simétrico de segundo orden: el tensor de tensiones. Este tensor de tensiones determina cuál es el vector tensión según la orientación con la que se mide. Ciertas orientaciones, las de los planos octaédricos, son muy notables.
Los planos octaédricos y las tensiones octaédricas
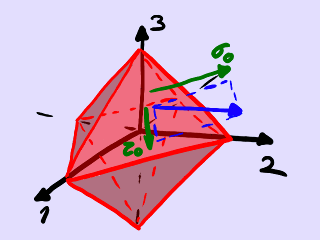
Planos octaédricos y tensiones octaédricas.
Vamos a tomar como sistema de referencia el definido por los ejes principales. En estos ejes, las componentes del tensor de tensiones adoptan la siguiente forma en representación matricial:
| σ1 | 0 | 0 |
| 0 | σ2 | 0 |
| 0 | 0 | σ3 |
Hay 4 direcciones diferentes que forman ángulos iguales con las direcciones principales o, si distinguimos entre las 2 orientaciones posibles para cada una de estas 4 direcciones, hay 8 posibilidades en total. Estas 8 orientaciones definen 8 planos como las 8 caras de un octaedro, así que son conocidas como las direcciones octaédricas. En ejes principales, las componentes de estas direcciones octaédricas son
(n1, n2, n3) = (±1 ⁄ √3, ±1 ⁄ √3, ±1 ⁄ √3).
Las componentes del vector tensión para una dirección octaédrica cualquiera son
(t1, t2, t3) = (±σ1±σ2±σ3) ⁄ √3.
El cuadrado de la magnitud del vector tensión es
|t|2 = (t1)2 + (t2)2 + (t3)2 = [(σ1)2+(σ2)2+(σ3)2] ⁄ 3.
La magnitud de la tensión octaédrica normal (la componente normal del vector tensión en la dirección perpendicular a un plano octaédrico) es
σo ≡ t1 n1 + t2 n2 + t3 n3 = (σ1+σ2+σ3) ⁄ 3 = σh = I1 ⁄ 3.
La tensión octaédrica normal es la tensión hidrostática, un tercio del primer invariante del tensor de tensiones.
La magnitud de la tensión octaédrica tangencial (la componente tangencial del vector tensión en la dirección perpendicular a un plano octaédrico) es
τo ≡ √[|t|2−(σo)2] = (1⁄3) √[(σ1−σ2)2 + (σ2−σ3)2 + (σ3−σ1)2] = √[(2⁄3) J2].
La tensión octaédrica tangencial es proporcional a la raíz cuadrada del segundo invariante del tensor desviador.
Aunque hay 8 planos octaédricos diferentes, las proyecciones normales y tangenciales del vector tensión medido en ellos son independientes del plano octaédrico elegido.
Categorías: Física
Permalink: http://sgcg.es/articulos/2015/08/31/tensiones-o-esfuerzos-mecanicos-10/
Tensiones o esfuerzos mecánicos (9)
2015-08-30
La mecánica de los medios continuos se ocupa del estudio del comportamiento macroscópico de los sólidos y los fluidos no como sistemas de partículas sueltas, sino como medios infinitamente divisibles. Se trata de una disciplina que, además de poder ser interesante por sus propios méritos, es la base de buena parte de nuestro actual desarrollo tecnológico. Uno de los conceptos más importantes de la mecánica de los medios continuos es el del tensor de tensiones o esfuerzos, que es una descripción matemática del estado de fuerzas por unidad de superficie en el seno de un medio continuo. Vimos recientemente que las tensiones en un medio continuo quedan caracterizadas mediante un tensor simétrico de segundo orden: el tensor de tensiones. Hoy veremos qué son la tensión hidrostática y el tensor desviador.
Tensión hidrostática y tensor desviador
Imaginemos un medio sometido únicamente a una presión hidrostática p. La presión isótropa y es lo único que constituye el estado tensional de este medio, así que el tensor de tensiones también es isótropo: el vector tensión medido en cualquier dirección tiene siempre la misma magnitud. Esto se cumple con un tensor de tensiones diagonal cuya representación matricial es como sigue:
| −p | 0 | 0 |
| 0 | −p | 0 |
| 0 | 0 | −p |
Es decir, el resultado de multiplicar la matriz unidad por un escalar (la presión con signo negativo, ya que las tensiones están tomadas por convenio como positivas cuando tiran hacia el exterior del volumen y las presiones están tomadas como positivas cuando empujan hacia el interior).
En el caso anterior, la presión (o, más bien, su negada) es igual a un tercio de la traza del tensor de tensión. Por extensión, se define la tensión hidrostática como un tercio de la traza del tensor de tensiones. Si le asignamos el símbolo σh, se define así con la notación de componentes tensoriales habitual de esta serie de artículos:
σh ≡ (1 ⁄ 3) (σ11+σ22+σ33) = I1 ⁄ 3.
Es decir, la tensión hidrostática es igual a un tercio del primer invariante del tensor de tensiones, ya que este primer invariante es la traza. La tensión hidrostática es independiente de la orientación del sistema de coordenadas.
No está de más desarrollar el tensor de tensiones como la suma de dos componentes: uno isótropo cuya diagonal está formada por la tensión hidrostática (cuyas componentes no varían al rotar el sistema de coordenadas) y otro, que llamaremos tensor desviador, cuyas componentes adoptan el valor
sij ≡ σij − σh δij,
donde δij es la delta de Kronecker, que adopta el valor 1 en los elementos diagonales (cuando i = j y el valor 0 en los demás elemento.
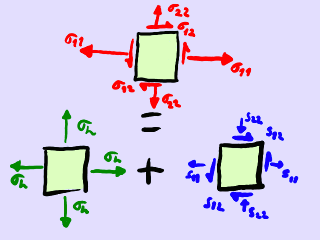
Descomposición del tensor de tensiones en tensión hidrostática y
tensión desviadora. El cuadrado es un volumen elemental de un medio
continuo que está sometido a tensiones (representadas mediante flechas
perpendiculares a las caras en el caso de las tensiones normales y
paralelas a las caras en el caso de las tensiones tangenciales).
La tensión desviadora tiene invariantes igual que los tiene el tensor de tensiones. Estos invariantes son los coeficientes del polinomio característico del tensor desviador, que podemos representar simbólicamente de forma análoga a la del polinomio característico del tensor de tensiones:
λ3 − J1 λ2 + J2 λ − J3.
Estos invariantes tienen los siguientes valores:
J1 ≡ 0;
J2 ≡ [(σ11−σ22)2 + (σ22−σ33)2 +; (σ33−σ11)2] ⁄ 6 + (σ12)2 + (σ23)2 + (σ13)2 = (I1)2 ⁄ 3 − I2.
J3 ≡ (2 ⁄ 27) [(σ11)3+(σ22)3+(σ33)3] − (1 ⁄ 9) [(σ11+σ22) (σ33)2 + (σ22+σ33) (σ11)2 + (σ33+σ11) (σ22)2] + (4 ⁄ 9) σ11 σ22 σ33 = (2 ⁄ 27) (I1)3 − (1 ⁄ 3) I1 I2 + I3.
Categorías: Física
Permalink: http://sgcg.es/articulos/2015/08/30/tensiones-o-esfuerzos-mecanicos-9/
Tensiones o esfuerzos mecánicos (8)
2015-08-22
La mecánica de los medios continuos se ocupa del estudio del comportamiento macroscópico de los sólidos y los fluidos no como sistemas de partículas sueltas, sino como medios infinitamente divisibles. Se trata de una disciplina que, además de poder ser interesante por sus propios méritos, es la base de buena parte de nuestro actual desarrollo tecnológico. Uno de los conceptos más importantes de la mecánica de los medios continuos es el del tensor de tensiones o esfuerzos, que es una descripción matemática del estado de fuerzas por unidad de superficie en el seno de un medio continuo. Vimos recientemente que las tensiones en un medio continuo quedan caracterizadas mediante un tensor simétrico de segundo orden: el tensor de tensiones. La fuerza por unidad de superficie medida resulta de aplicar este tensor sobre la dirección perpendicular a la superficie de medida y, en general, no es paralela a dicha dirección. Ayer echamos un vistazo a lo que son las tensiones principales y las direcciones principales. Hoy vamos a estudiar algo relacionado con este último concepto: los invariantes del tensor de tensiones, unas magnitudes que son independientes de la dirección y el sistema de coordenadas (por ser propiedades intrínsecas del tensor de tensiones).
Invariantes
Ayer establecimos que el cálculo de las tensiones principales y las direcciones principales se reduce al siguiente problema de autovalores en el que las incógnitas son las componentes n1, n2 y n3 de la dirección principal y el valor λ de la tensión principal:
σ11 n1 + σ12 n2 + σ13 n3 = λ n1;
σ12 n1 + σ22 n2 + σ23 n3 = λ n2;
σ13 n1 + σ23 n2 + σ33 n3 = λ n3.
Si fijamos un valor arbitrario de la variable λ, queda un sistema de 3 ecuaciones con 3 incógnitas cuya solución en general es trivial: las componentes de la dirección son todas nulas. Ahora bien, hay unos pocos valores de la variable λ, los autovalores del problema, que hacen que el sistema de ecuaciones sea indeterminado y pueda tener soluciones distintas a la trivial. Estos autovalores son las tensiones principales. Una forma de calcularlos es hacer nulo el determinante de la matriz del sistema de ecuaciones. Este determinante es el polinomio característico del sistema de ecuaciones y es de tercer grado. La ecuación a resolver (la ecuación característica) tiene la siguiente forma:
−λ3 + I1 λ2 − I2 λ + I3,
donde
I1 ≡ σ11 + σ22 + σ33;
I2 ≡ σ11 σ22 + σ22 σ33 + σ33 σ11 − (σ12)2 − (σ23)2 − (σ13)2.
I3 ≡ σ11 σ22 σ33 + 2 σ12 σ23 σ13 − σ11 (σ23)2 − σ22 (σ13)2 − σ33 (σ12)2.
El polinomio característico es invariante ante transformaciones de semejanza. Si rotamos el sistema de coordenadas, la nueva matriz de tensiones, ya que es la representación de un tensor, sale de aplicar una transformación de semejanza a la original. Por lo tanto, el polinomio característico es invariante ante rotaciones del sistema de coordenadas. Esto significa que las magnitudes I1, I2 e I3 son independientes de la orientación del sistema de coordenadas: son los invariantes del tensor de tensiones. Por supuesto, el tensor de tensiones en un punto no tiene por qué ser igual al tensor de tensiones en otro punto, así que los invariantes sí pueden variar en función del punto en el que están medidos.
Digamos que tenemos tres soluciones de la incógnita λ del polinomio característico: σ1, σ2 y σ3. Se trata de las tensiones principales. En un sistema de referencia cuyos ejes coordenados son las direcciones principales, la matriz de tensiones que representa al tensor de tensiones en tal eje es diagonal y tiene la siguiente forma:
| σ1 | 0 | 0 |
| 0 | σ2 | 0 |
| 0 | 0 | σ3 |
En este sistema de ejes principales, los invariantes son más fáciles de calcular, aunque tienen el mismo valor numérico que siempre:
I1 ≡ σ1 + σ2 + σ3;
I2 = σ1 σ2 + σ2 σ3 + σ3 σ1;
I3 ≡ σ1 σ2 σ3.
Categorías: Física
Permalink: http://sgcg.es/articulos/2015/08/22/tensiones-o-esfuerzos-mecanicos-8/
Tensiones o esfuerzos mecánicos (7)
2015-08-21
La mecánica de los medios continuos se ocupa del estudio del comportamiento macroscópico de los sólidos y los fluidos no como sistemas de partículas sueltas, sino como medios infinitamente divisibles. Se trata de una disciplina que, además de poder ser interesante por sus propios méritos, es la base de buena parte de nuestro actual desarrollo tecnológico. Uno de los conceptos más importantes de la mecánica de los medios continuos es el del tensor de tensiones o esfuerzos, que es una descripción matemática del estado de fuerzas por unidad de superficie en el seno de un medio continuo. Vimos recientemente que las tensiones en un medio continuo quedan caracterizadas mediante un tensor simétrico de segundo orden: el tensor de tensiones. La fuerza por unidad de superficie medida resulta de aplicar este tensor sobre la dirección perpendicular a la superficie de medida y, en general, no es paralela a dicha dirección. Ahora bien, hay ciertos planos para los que la tensión medida sí es paralela a la dirección perpendicular. Las tensiones correspondientes son las tensiones principales y las direcciones de medida son las direcciones principales.
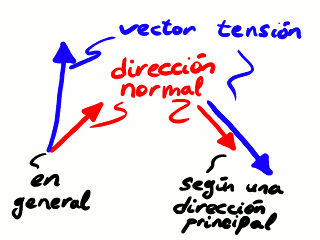
Concepto de dirección principal y tensión principal.
Tensiones principales
El vector tensión t medido en la dirección normal n cuando el tensor de tensiones es σ sale de la siguiente relación:
t = σ ⋅ n.
En general, el vector tensión y el vector normal no son necesariamente paralelos. Ahora bien, hay algunas direcciones (las direcciones principales) para las que sí se cumple que los vectores tensión salen paralelos a ellas. Podemos escribir la condición de paralelismo de la siguiente manera:
t = λ n = σ ⋅ n.
La constante de proporcionalidad λ es la tensión principal correspondiente a la dirección principal. En notación de componentes, tenemos las siguientes ecuaciones en las que es importante el uso de la simetría del tensor de tensiones.
σ11 n1 + σ12 n2 + σ13 n3 = λ n1;
σ12 n1 + σ22 n2 + σ23 n3 = λ n2;
σ13 n1 + σ23 n2 + σ33 n3 = λ n3.
En estas tres ecuaciones, tanto las componentes n1, n2 y n3 de la dirección principal como la tensión principal λ son incógnitas. Se trata de un problema autovalores convencional que puede tener hasta 3 soluciones linealmente independientes. Las direcciones principales son ortogonales entre sí. Para comprobarlo, tomemos 2 direcciones principales representadas por las matrices columna n1 y n2 (no hay que confundirlas con la notación de componentes de antes) que llevan sus componentes en coordenadas cartesianas. Las tensiones principales correspondientes son λ1 y λ2. El tensor tensión está representado por la matriz simétrica σ con sus componentes en coordenadas cartesianas. Tenemos las siguientes relaciones:
(σ−λ1) n1 = 0;
(σ−λ2) n2 = 0.
Si premultiplicamos la primera por (n2)T (la traspuesta de n2) y la segunda ecuación por (n1)T (la traspuesta de n1), queda lo siguiente:
(n2)T (σ−λ1) n1 = 0;
(n1)T (σ−λ2) n2 = 0.
Tomemos la traspuesta de la segunda ecuación. Gracias a la simetría de la matriz de tensiones, queda así:
(n2)T (σ−λ2) n1 = 0.
Restemos la primera ecuación y esta traspuesta de la segunda ecuación:
(n2)T [(σ−λ1) − (σ−λ2)] n1 = (λ1−λ2) (n2)T n1 = 0.
Si las tensiones principales escogidas son diferentes, el producto de las direcciones principales es nulo, lo que implica que son perpendiculares. Si varias tensiones principales son iguales, entonces las direcciones principales no están completamente definidas, ya que es posible rotarlas arbitrariamente dentro del espacio en el que se mueven.
Digamos que tenemos tres soluciones de la incógnita λ del polinomio característico: σ1, σ2 y σ3. Se trata de las tensiones principales. En un sistema de referencia cuyos ejes coordenados son las direcciones principales, la matriz de tensiones que representa al tensor de tensiones en tal eje es diagonal y tiene la siguiente forma:
| σ1 | 0 | 0 |
| 0 | σ2 | 0 |
| 0 | 0 | σ3 |
En ejes principales, no hay tensiones tangenciales o cortantes.
La transformación de un sistema de coordenadas al otro se hace mediante una transformación de semejanza normal y corriente. Si σ es la matriz de tensiones en la base original, σ' es la matriz de diagonal en la base de los ejes principales y N es la matriz con los autovectores normalizados (una matriz cuyas columnas son las componentes de las direcciones principales, cada columna con norma euclídea unidad), el cambio de base se realiza así:
σ' = C−1 σ C.
Ahora bien, como los ejes principales son ortonormales, la matriz de cambio de base es ortogonal y la expresión es todavía más sencilla, ya que la inversión se reduce a una trasposición:
σ' = CT σ C.
Categorías: Física
Permalink: http://sgcg.es/articulos/2015/08/21/tensiones-o-esfuerzos-mecanicos-7/
Tensiones o esfuerzos mecánicos (6)
2015-08-19
La mecánica de los medios continuos se ocupa del estudio del comportamiento macroscópico de los sólidos y los fluidos no como sistemas de partículas sueltas, sino como medios infinitamente divisibles. Se trata de una disciplina que, además de poder ser interesante por sus propios méritos, es la base de buena parte de nuestro actual desarrollo tecnológico. Uno de los conceptos más importantes de la mecánica de los medios continuos es el del tensor de tensiones o esfuerzos, que es una descripción matemática del estado de fuerzas por unidad de superficie en el seno de un medio continuo. Vimos recientemente que las tensiones en un medio continuo quedan caracterizadas mediante un tensor de segundo orden: el tensor de tensiones. Hoy determinaremos que se trata de un tensor simétrico.
La conservación del momento angular y la simetría del tensor de tensiones
Vamos a hacer un trabajo análogo al del artículo de ayer y vamos a plantear la ley del momento angular. Vamos a usar la misma notación que entonces con la única novedad del vector r, que es el radio vector de cada punto del dominio en el que integramos. Este radio vector tiene componentes x1, x2 y x3 en el sistema de coordenadas cartesianas que vamos a utilizar. Tenemos lo siguiente:
∫∫∫V ρ r × a dV = ∫∫∫V r × f dV + ∫∫S r × n ⋅ σ dS.
Si asumimos que el campo de tensiones es diferenciable y aplicamos el teorema de la divergencia, la integral de superficie se convierte en una integral de volumen:
∫∫S r × n ⋅ σ dS = ∫∫∫V div[r × σ] dV = ∫∫∫V (grad r) × σ dV + ∫∫∫V r × (div σ) dV.
La notación del producto vectorial entre el gradiente del radio vector y el tensión de tensiones es un poco artificial; la expresión es un vector cuya componente i-ésima es
[(grad r) × σ]i = ∑j∑k∑l εijk ∂rj ⁄ ∂rl σlk = ∑j∑k εijk σjk.
En la expresión anterior, εijk es el símbolo de Levy-Civita, que adopta un valor nulo para todas las combinaciones de índices menos para los siguientes casos:
ε123 = ε312 = ε231 = 1;
ε321 = ε132 = ε213 = −1.
Volvamos al resultado del teorema de la divergencia. Sustituyamos el valor de la igualdad en la ley del momento angular y agrupemos términos:
0 = ∫∫∫V r × [−ρ a + f + div σ] dV + ∫∫∫V (grad r) × σ dV.
El dominio de integración V. Por lo tanto, para que se cumpla la primera integral, tiene que cumplirse la ecuación diferencial
[r × (−ρ a + f + div σ] + [(grad r) × σ] = 0,
Hay dos términos entre corchetes. El primer término es el producto exterior del radio vector y los términos no explícitamente nulos de la ecuación de la cantidad de movimiento en forma diferencial, así que sabemos que es igual a 0. Tras cancelar, queda el otro término, que todavía aporta información interesante:
(grad r) × σ = 0.
Las tres componentes de esta magnitud salen de desarrollar la expresión que vimos antes en la que aparecía el símbolo de Levy-Civita:
σ23 − σ32 = 0;
σ31 − σ13 = 0;
σ12 − σ21 = 0.
Por lo tanto, el tensor de tensiones es simétrico.
Categorías: Física
Permalink: http://sgcg.es/articulos/2015/08/19/tensiones-o-esfuerzos-mecanicos-6/
Tensiones o esfuerzos mecánicos (5)
2015-08-18
La mecánica de los medios continuos se ocupa del estudio del comportamiento macroscópico de los sólidos y los fluidos no como sistemas de partículas sueltas, sino como medios infinitamente divisibles. Se trata de una disciplina que, además de poder ser interesante por sus propios méritos, es la base de buena parte de nuestro actual desarrollo tecnológico. Uno de los conceptos más importantes de la mecánica de los medios continuos es el del tensor de tensiones o esfuerzos, que es una descripción matemática del estado de fuerzas por unidad de superficie en el seno de un medio continuo. En el último artículo vimos que las tensiones en un medio continuo quedan caracterizadas mediante un tensor de segundo orden: el tensor de tensiones. Anteriormente, vimos de forma fugaz la ecuación de la cantidad de movimiento en forma integral para una masa de control. Hoy vamos con la fora diferencial, que será útil más adelante.
Ley de la cantidad de movimiento en forma diferencial
Retomemos la ecuación de la cantidad de movimiento que aparecía en el tercer artículo de esta serie:
∫∫∫V ρ a dV = ∫∫∫V f dV + ∫∫S t dS.
El vector tensión t está relacionado con la normal n al contorno del dominio y el tensor de tensiones σ mediante la ley
t = n ⋅ σ.
Con esto, la ley de la cantidad de movimiento queda de la siguiente manera:
∫∫∫V ρ a dV = ∫∫∫V f dV + ∫∫S n ⋅ σ dS.
Si asumimos que el campo de tensiones es diferenciable y aplicamos el teorema de la divergencia, la integral de superficie se convierte en una integral de volumen:
∫∫S n ⋅ σ dS = ∫∫∫V div σ dV.
Sustituyamos el valor de esta igualdad en la ley de la cantidad de movimiento y agrupemos términos:
0 = ∫∫∫V −ρ a + f + div σ dV.
El dominio de integración V. Por lo tanto, para que se cumpla la primera integral, tiene que cumplirse la ecuación diferencial
−ρ a + f + div σ = 0.
Esta ecuación es la ley de conservación de la cantidad de movimiento en forma diferencial. La formulación es lagrangiana (ligada al material) así que la aceleración quedaría sustituida por la derivada convectiva de la velocidad en una descripción euleriana (ligada al espacio).
Categorías: Física
Permalink: http://sgcg.es/articulos/2015/08/18/tensiones-o-esfuerzos-mecanicos-5/
Tensiones o esfuerzos mecánicos (4)
2015-08-16
La mecánica de los medios continuos se ocupa del estudio del comportamiento macroscópico de los sólidos y los fluidos no como sistemas de partículas sueltas, sino como medios infinitamente divisibles. Se trata de una disciplina que, además de poder ser interesante por sus propios méritos, es la base de buena parte de nuestro actual desarrollo tecnológico. Uno de los conceptos más importantes de la mecánica de los medios continuos es el del tensor de tensiones o esfuerzos, que es una descripción matemática del estado de fuerzas por unidad de superficie en el seno de un medio continuo. En el último artículo vimos que el estado tensional en un punto queda completamente caracterizado mediante una aplicación lineal sobre la dirección de medida. Hoy veremos que, como consecuencia de ello, las tensiones quedan descritas mediante un tensor de orden 2.
El tensor de tensiones
En vez de llamar a los ejes y a las componentes x, y y z como en el artículo anterior, hoy vamos a usar números: están los ejes 1, 2 y 3, de manera que el vector normal n que indica la dirección de medida tiene componentes n1, n2 y n3. Algo análogo puede decirse del vector tensión. En cuanto a las componentes de la aplicación lineal que representa las tensiones, tenemos σ11, σ12, …, σ65 y σ66. La componente j-ésima del vector tensión medido en la dirección n es
tj = ∑i ni σij.
Ahora supongamos que queremos pasar a un sistema de ejes rotado según la ley de transformación siguiente:
n'i = ∑j cij nj.
Es decir, se aplica una matriz de rotación de componentes {cij}. Los índices de las magnitudes rotadas se refieren a las componentes en los ejes rotados, no en los ejes originales. La transformación para el vector tensión es igual:
t'i = ∑j cij tj.
Asumimos que en el nuevo sistema de referencia hay unas componentes rotadas de la matriz que representa las tensiones:
t'j = ∑i n'i σ'ij.
Ahora bien, el vector tensión en ejes rotados puede expresarse en función del vector tensión en los ejes originales:
∑k cjk tk = ∑i n'i σ'ij.
De igual manera, el vector normal en ejes rotados puede expresarse en función del vector normal en los ejes originales:
∑k cjk tk = ∑i ∑l cil nl σ'ij.
Si multiplicamos a ambos lados de la igualdad por la inversa de la matriz de cambio de base, queda lo siguiente:
tk = ∑i ∑k∑l c−1kj cil nl σ'ij.
Ahora bien, esta ecuación es la relación entre normal y vector tensión en los ejes iniciales si definimos la siguiente rotación:
σij = ∑k ∑l c−1jk cli σ'lk.
Un objeto geométrico cuyas componentes se transforman de unos ejes a otros mediante este tipo de ley es un tensor. Las tensiones están completamente determinadas mediante un campo tensorial de orden 2.
Hasta ahora, hemos trabajado en ejes cartesianos, así que no hay diferencia entre componentes covariantes y componentes contravariantes. Con la notación de índices mudos de Einstein, tenemos las siguientes relaciones entre las componentes del vector tensión y las del vector normal tanto covariantes como contravariantes:
ti = nj σji;
ti = nj σji.
Categorías: Física
Permalink: http://sgcg.es/articulos/2015/08/16/tensiones-o-esfuerzos-mecanicos-4/
Tensiones o esfuerzos mecánicos (3)
2015-08-14
La mecánica de los medios continuos se ocupa del estudio del comportamiento macroscópico de los sólidos y los fluidos no como sistemas de partículas sueltas, sino como medios infinitamente divisibles. Se trata de una disciplina que, además de poder ser interesante por sus propios méritos, es la base de buena parte de nuestro actual desarrollo tecnológico. Uno de los conceptos más importantes de la mecánica de los medios continuos es el del tensor de tensiones o esfuerzos, que es una descripción matemática del estado de fuerzas por unidad de superficie en el seno de un medio continuo. En el primer artículo empezamos a ver el concepto de las fuerzas por unidad de superficie en el seno de un medio continuo: el vector tensión cuyas componentes vimos en el artículo de ayer. Hoy vamos a ver cómo representar las tensiones mediante una aplicación lineal.
Las tensiones como aplicación lineal
Analicemos lo que ocurre en un subdominio infinitesimal en el seno de un medio continuo. Este subdominio tiene forma de tetraedro como en la siguiente figura:
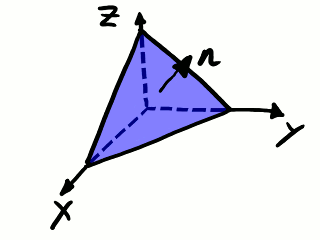
Subdominio tetraédrico. Tres caras son perpendiculares entre sí y
sirven para definir un sistema de coordenadas.
Este subdominio de volumen V y superficie de contorno S está sometido a fuerzas por unidad de superficie t (las tensiones) por su contorno y a fuerzas distribuidas f por su volumen. Bajo la acción de estas fuerzas, el material, que tiene una densidad ρ, experimenta una aceleración a de acuerdo con la ley de la cantidad de movimiento:
∫∫∫V ρ a dV = ∫∫∫V f dV + ∫∫S t dS.
Ahora escalemos el tetraedro hasta hacerlo muy, muy pequeño. El volumen va con el cubo del factor de escala, mientras que la superficie del contorno va con el cuadrado del factor de escala. Por lo tanto, las integrales de volumen van con la tercera potencia de una cantidad muy pequeña, mientras que la integral de superficie va solamente con la segunda potencia. Las integrales de volumen se convierten en infinitésimos despreciables frente a la integral de superficie y, en el límite, nos quedamos solamente con esta última integral, la de las tensiones.
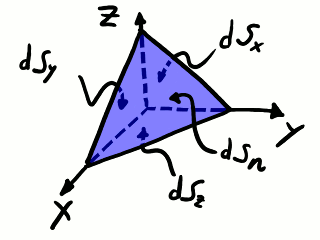
Subdominio tetraédrico infinitesimal.
Describamos un poco la geometría de nuestro tetraedro infinitesimal, que tiene tres caras perpendiculares entre sí de manera que definen un triedro que nos sirve para establecer un sistema de coordenadas cartesianas. Las normales exteriores a estas caras apuntan en las direcciones de los ejes coordenados en sentido negativo. La cara perpendicular al eje X tiene superficie dSx. La cara perpendicular al eje Y tiene superficie dSy. La cara perpendicular al eje Z tiene superficie dSz. La cuarta cara, cuya normal es n, tiene superficie eje X tiene superficie dSn. Las componentes del vector normal n a esta cara son nx según el eje X, ny según el eje Y y nz según el eje Z. Las superficies de las tres primeras caras están relacionadas con la superficie de la cuarta cara a través de las componentes de la normal que acabamos de definir:
dSx = dSn nx;
dSy = dSn ny;
dSz = dSn nz.
Listas las definiciones geométricas, ahora hace falta establecer la notación para las tensiones. La tensión medida en la cara perpendicular al eje X tiene componentes σxx (según el eje X negativo), σxy (según el eje Y negativo) y σxz (según el eje Z negativo). La tensión medida en la cara perpendicular al eje Y tiene componentes σyx (según el eje X en sentido negativo), σyy (según el eje Y en sentido negativo) y σyz (según el eje Z en sentido negativo). La tensión medida en la cara perpendicular al eje Z tiene componentes σzx (según el eje X en sentido negativo), σzy (según el eje Y en sentido negativo) y σzz (según el eje Z en sentido negativo). Finalmente, la tensión medida en la cuarta cara tiene componentes tx (según el eje X en sentido positivo), ty (según el eje Y en sentido positivo) y tz (según el eje Z en sentido positivo). Este criterio de signos, con las componentes en sentido negativo en las tres primeras caras y en sentido positivo en la cuarta cara, es para que nos queden las cuentas un poco más ordenadas al plantear la ecuación de la cantidad de movimiento.
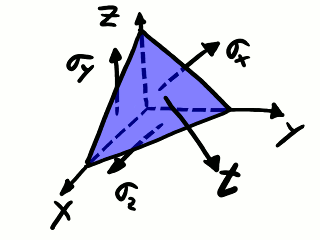
Tetraedro infinitesimal bajo tensiones.
Ahora que está todo definido, podemos plantear la ecuación de la cantidad de movimiento. Vimos que los términos volumétricos eran despreciables y solamente quedaban las integrales de superficie de las tensiones. Para un volumen infinitesimal, salen tres ecuaciones, una por cada componente:
0 = −σxx dSx − σyx dSy − σzx dSz + tx dSn;
0 = −σxy dSx − σyy dSy − σzy dSz + ty dSn;
0 = −σxz dSx − σyz dSy − σzz dSz + tz dSn.
Ahora bien, las superficies dSx, dSy y dSz están relacionadas con dSn como vimos antes. Podemos introducir las relaciones en las ecuaciones de la cantidad de movimiento y dejarlas así:
0 = −σxx dSn nx − σyx dSn ny − σzx dSn nz + tx dSn;
0 = −σxy dSn nx − σyy dSn ny − σzy dSn nz + ty dSn;
0 = −σxz dSn nx − σyz dSn ny − σzz dSn nz + tz dSn.
Esto es lo mismo que decir lo siguiente:
tx = σxx nx + σyx ny + σzx nz;
ty = σxy nx + σyy ny + σzy nz;
tz = σxz nx + σyz ny + σzz nz.
La dirección n es cualquiera que escojamos, así que tenemos una ley general que explica cómo varía el vector de tensión en función de la dirección en la que se mide. Esta ley es una aplicación lineal sobre el vector unitario que marca la dirección. Podemos dejar escrita esta relación de forma matricial:
tT = nT ⋅ σ.
En esta relación, tT es el vector tensión representado como una matriz fila:
| tx | ty | tz |
| nx | ny | nz |
| σxx | σxy | σxz |
| σyx | σyy | σyz |
| σzx | σzy | σzz |
Esto es tan importante que hay que repetirlo. En un punto dado, el vector tensión se calcula mediante una aplicación lineal sobre el vector unitario que marca la dirección de medida; esta aplicación lineal está representada mediante las componentes de una matriz cuadrada. Más adelante, veremos que lo propio es hablar de un tensor cuadradade tensiones.
Categorías: Física
Permalink: http://sgcg.es/articulos/2015/08/14/tensiones-o-esfuerzos-mecanicos-3/
Tensiones o esfuerzos mecánicos (2)
2015-08-13
La mecánica de los medios continuos se ocupa del estudio del comportamiento macroscópico de los sólidos y los fluidos no como sistemas de partículas sueltas, sino como medios infinitamente divisibles. Se trata de una disciplina que, además de poder ser interesante por sus propios méritos, es la base de buena parte de nuestro actual desarrollo tecnológico. Uno de los conceptos más importantes de la mecánica de los medios continuos es el del tensor de tensiones o esfuerzos, que es una descripción matemática del estado de fuerzas por unidad de superficie en el seno de un medio continuo. En el anterior artículo empezamos a ver el concepto de las fuerzas por unidad de superficie en el seno de un medio continuo. Hoy continuamos con el vector tensión y sus componentes.
El vector tensión y sus componentes
Tal como vimos ayer, si elegimos un punto cualquiera en el seno de un medio continuo y una orientación, encontramos allí un vector de fuerza por unidad de superficie. Esta fuerza por unidad de superficie es el vector de la tensión. El vector tensión es un campo vectorial que depende de la posición y de la orientación.
La orientación de la que hablamos, como vimos, está caracterizada por un vector unitario que apunta en la dirección perpendicular hacia el exterior de la superficie que sirve de contorno para un subdominio del medio continuo.
Elegidas una posición y una orientación, el vector tensión puede dividirse en general en dos componentes: una componente alineada con la orientación y otra componente perpendicular a la orientación. Como el vector orientación es el vector normal a una superficie, la componente del vector tensión alineada con la orientación es la componente normal a la superficie. De igual manera, la otra componente es la componente tangente a la superficie. Hablamos, pues, de tensiones normales y tensiones tangenciales. Las tensiones normales también se llaman directas y las tensiones tangenciales también se llaman cortantes o de cizalladura.
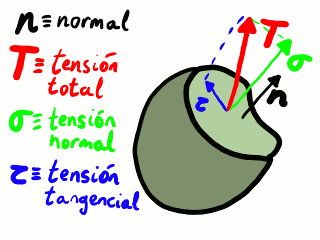
Componentes de la tensión.
Categorías: Física
Permalink: http://sgcg.es/articulos/2015/08/13/tensiones-o-esfuerzos-mecanicos-2/
Tensiones o esfuerzos mecánicos (1)
2015-08-12
La mecánica de los medios continuos se ocupa del estudio del comportamiento macroscópico de los sólidos y los fluidos no como sistemas de partículas sueltas, sino como medios infinitamente divisibles. Se trata de una disciplina que, además de poder ser interesante por sus propios méritos, es la base de buena parte de nuestro actual desarrollo tecnológico. Uno de los conceptos más importantes de la mecánica de los medios continuos es el del tensor de tensiones o esfuerzos, que es una descripción matemática del estado de fuerzas por unidad de superficie en el seno de un medio continuo. En este artículo y los siguientes veremos en qué consiste.
Fuerzas por unidad de superficie
Los medios continuos que estudiamos son medios materiales, sustancias que interactúan unas con otras mediante fuerzas. Hay fuerzas de largo alcance, como la fuerza de gravedad, pero también hay fuerzas de tan corto alcance que podemos modelarlas como fuerzas de contacto: se producen al tocar un cuerpo con otro.
Imaginémonos un medio continuo. Cortémoslo imaginariamente en dos partes mediante un plano. Cada una de estas partes o subdominios, A y B, es un medio continuo en contacto con la otra parte a través del plano de corte. Más adelante, nos referiremos a la superficie de contacto como S.
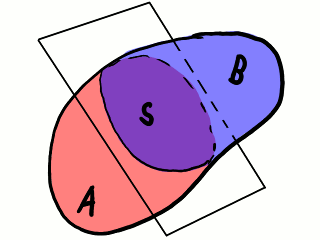
División de un medio continuo en dos partes mediante un plano de
corte.
Uno de los subdominios, A, es objeto de una fuerza de contacto F a través de la superficie de corte S. Por el principio de acción y reacción, el otro subdominio, B, recibe una fuerza de contacto igual y opuesta, −F. Como todas las fuerzas, F es vectorial: tiene una magnitud y una dirección. En general, la dirección de la fuerza de contacto no es necesariamente perpendicular a la superficie de contacto: tiene una componente normal y una componente tangencial.
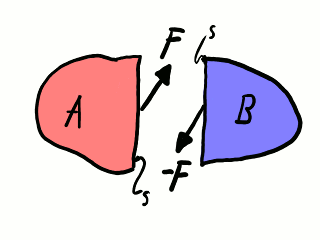
Fuerzas de contacto internas.
Más que las fuerzas totales en una superficie de contacto, nos interesan las fuerzas por unidad de superficie. Antes teníamos una fuerza de contacto F (del subdominio B sobre el subdomio A) aplicada en una superficie de contacto que llamaremos S; la fuerza de contacto promediada por la superficie de contacto es F ⁄ S. Nada nos impide dividir o teselar la superficie de contacto en superficies más pequeñas como si fuera un rompecabezas hecho de múltiples piezas; si lo hacemos, vemos que se aplica una fuerza de contacto a través de cada una de estas piezas de la superficie, de manera que la fuerza de contacto total es igual a la suma de las fuerzas aplicadas en las piezas. De igual manera, en cada pieza hay fuerza por unidad de superficie: la fuerza de contacto en esa pieza dividida por la superficie en esa pieza.
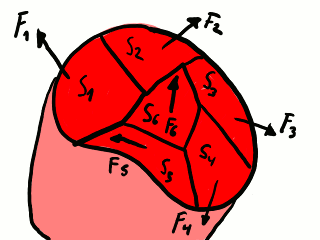
Teselación de un plano de corte.
Si llevamos el proceso al límite, las piezas quedan de un tamaño infinitesimal, cada una rodeando a un punto de la superficie de contacto. A cada uno de estos puntos le corresponde un vector de fuerza por unidad de superficie.
Fijémonos en un punto y hagamos pasar dos planos de corte con orientaciones diferentes por él. En general, no tenemos motivos para asumir que la fuerza por unidad de superficie con el primer plano de corte es igual a la fuerza por unidad de superficie con el segundo plano de corte: la fuerza por unidad de superficie depende del punto en el que la medimos y de la orientación con la que la medimos. La orientación viene dada por el vector normal a la frontera del subdominio, que por convenio apunta hacia el exterior. Si invertimos la orientación es como si pasamos de un subdominio al complementario (del A al B) y la fuerza por unidad de superficie cambia también de sentido. No hace falta definir subdominios para hablar de fuerzas por unidad de superficie: basta indicar el punto en el que se mide y la orientación con la que se mide.
Categorías: Física
Permalink: http://sgcg.es/articulos/2015/08/12/tensiones-o-esfuerzos-mecanicos-1/
Breve apunte sobre las emociones en los animales
2015-08-08
Muchos animales, ante determinados estímulos, desarrollan comportamientos que sugieren una respuesta emocional análoga a la que experimentaría un ser humano en similares circunstancias. A menudo, es un error seguir una perspectiva antropomórfica y asociar estados mentales humanos a unos animales que en realidad son diferentes. Ahora bien, de igual manera, puede ser un error descartar todo rastro de estado emocional por el mero hecho de tratar con una criatura distinta.
Si aplicamos ingenuamente una perspectiva antropomórfica, podemos asociar por error unas emociones humanas a algo que en realidad es diferente. Un ejemplo de este tipo de error que se ha hecho popular recientemente es el de un lori perezoso (un pequeño primate del sur de Asia) en cautiverio que apareció en un vídeo en el que un ser humano le hacía cosquillas; el animal se quedaba quieto con los brazos en alto, lo que a no pocas personas les sugirió que estaba disfrutando de la situación, cuando en realidad mostraba una reacción defensiva. Este ejemplo, apenas uno entre los muchos que hay, sirve como aviso: no hay que caer en el error del antropomorfismo ingenuo.
Lo dicho en el anterior párrafo no implica, sin embargo, que los animales, por ser diferentes, carezcan de toda similitud con el ser humano. Vayamos por partes. En primer lugar, no es descabellado afirmar que los animales experimentan emociones genuinas. Si asumimos que los demás seres humanos tienen una conciencia, una experiencia subjetiva real, no hay motivos para pensar que el ser humano es especial y los animales, a pesar de contar con estructuras neurológicas y funcionamientos similares, son mecanismos vacíos de conciencia. Si acaso, lo que es descabellado es asumir que los humanos son especiales y los animales son zombis filosóficos: si el antropomorfismo puede ser un error, también puede ser un error el excepcionalismo humano. Además de esto y a pesar de lo visto en el párrafo anterior, sí hay estados mentales que son claramente análogos a los del ser humano, producen comportamientos similares y se disparan por las mismas causas: tal es el caso, por ejemplo, del miedo. También hay casos más oscuros y difíciles de clasificar: por ejemplo, muchos animales no humanos lloran, quizá no exactamente por tristeza, pero sin duda lo hacen al ser expuestos a situaciones que podrían hacer llorar a un ser humano, de manera que sería ingenuo suponer que el animal se encuentra satisfecho y alegre en ese estado.
La conclusión es que la interpretación del estado emocional de un animal no humano es una tarea que puede ser mucho más difícil que la equivalente en el caso de un ser humano. No siempre es legítimo antropomorfizar al animal, pero a veces sí lo es.
Categorías: Miscelánea
Permalink: http://sgcg.es/articulos/2015/08/08/breve-apunte-sobre-las-emociones-en-los-animales/
