Septiembre de 2017
Calendario de artículos de de 2017
| lu | ma | mi | ju | vi | sá | do |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | |
Deuda pública y comparaciones odiosas
2017-09-30
La deuda pública es una fuente de polémica. Proporciona la liquidez inmediata necesaria para acometer muchos proyectos, pero penaliza la liquidez futura. A menudo, el endeudamiento es el medio menos doloroso para cubrir una necesidad, pero también suele ser una fuente de problemas, por lo que hay que utilizarlo con sabiduría.
En estos tiempos de recortes, algunas administraciones han aumentado su deuda y otras la han reducido. En concreto, hay algún ayuntamiento «anti austeridad» que reduce su deuda a gran velocidad y cuyo caso inspira artículos de opinión que ensalzan su trabajo y ningunean el de la administración de la comunidad autónoma y la administración central, con endeudamientos crecientes. Quienes mandan en estas administraciones llevan una política de recortes, pero no parecen tener un gran éxito (por decirlo suavemente), al menos a primera vista. Esto inspira artículos que caen en explicaciones fáciles, pero inadecuadas: achacan la diferencia en los resultados a la corrupción e incompetencia de los «austerófilos» y a la incorruptibilidad y el buen hacer de los «austerófobos». Tal explicación es inadecuada debido a que compara administraciones de tamaños diferentes, con competencias diferentes y estructuras de costes e ingresos diferentes. Dentro de ciertos límites, puede ser legítimo comparar el trabajo del equipo de gobierno entrante con el del saliente en una determinada administración (digamos que en un ayuntamiento), pero no lo que hace un ayuntamiento con lo que hace una comunidad autónoma. Siempre existe la terrorífica posibilidad de que los gobernantes inútiles de una cierta administración desastrosa sean los menos inútiles de entre todos los posibles.
Categorías: Miscelánea
Permalink: http://sgcg.es/articulos/2017/09/30/deuda-publica-y-comparaciones-odiosas/
Deformaciones mecánicas (9)
2017-09-28
En general, los cuerpos y medios materiales no permanecen perfectamente quietos, sino que se mueven y cambian de forma según transcurre el tiempo como consecuencia de sus interacciones con el entorno y de su propia dinámica interna. Esta serie de artículos trata sobre los cambios de forma o deformaciones.
El tensor de deformación infinitesimal
Arrastramos la notación del anterior artículo. Partimos de un cuerpo material cuyos puntos, identificados por sus vectores de posición x en el estado inicial, experimentan un campo de desplazamientos u(x) hasta alcanzar en las posiciones x'(x).
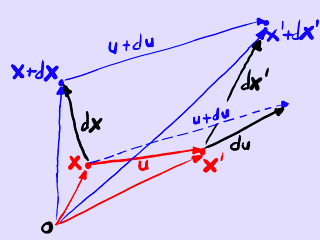
Concepto de variación infinitesimal del desplazamiento.
El tensor de deformación de Green-Lagrange tiene como desventaja que presenta un término cuadrático en el tensor de gradiente de desplazamiento. Convenientemente, en muchísimos casos de gran interés tecnológico, las componentes del tensor de gradiente de desplazamiento son tan pequeñas que es perfectamente legítimo despreciar los términos cuadráticos del tensor de deformación de Lagrange-Green. El tensor de deformación que sale de conservar exclusivamente los términos lineales del tensor de deformación Lagrange-Green es el tensor de deformación infinitesimal. Dado que el contexto permite identificar claramente de qué hablamos, lo designaremos con el símbolo ε, el mismo que usamos para el tensor de deformación de Green-Lagrange. El tensor de deformación infinitesimal se define así en función del tensor de gradiente de desplazamiento:
ε ≡ (1 ⁄ 2) [(∇u)T + ∇u].
La componente i,j-ésima de este tensor es
εij ≡ (1 ⁄ 2) (∂uj ⁄ ∂xi + ∂ui ⁄ ∂xj).
Igual que el tensor de deformación de Green-Lagrange, el tensor de deformación infinitesimal es simétrico. Es, de hecho, la parte simétrica del tensor de gradiente de desplazamiento:
∇u = (1 ⁄ 2) [∇u + ∇(u)T] + (1 ⁄ 2) [∇u − (∇u)T].
El primer sumando, simétrico por construcción, es el tensor de deformación infinitesimal. El segundo sumando, antimétrico por construcción, está relacionado con la rotación de sólido rígido, aunque también es no nulo en movimientos que no son rotaciones de sólido rígido: es una forma de expresar el rotacional del campo vectorial de desplazamientos.
Categorías: Física
Permalink: http://sgcg.es/articulos/2017/09/28/deformaciones-mecanicas-9/
Deformaciones mecánicas (8)
2017-09-26
En general, los cuerpos y medios materiales no permanecen perfectamente quietos, sino que se mueven y cambian de forma según transcurre el tiempo como consecuencia de sus interacciones con el entorno y de su propia dinámica interna. Esta serie de artículos trata sobre los cambios de forma o deformaciones.
El estiramiento
Arrastramos la notación del anterior artículo.
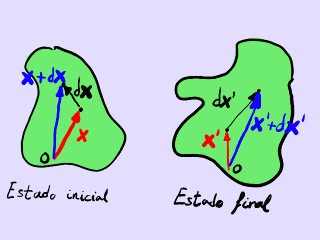
Deformación de un segmento infinitesimal.
Partamos de un segmento infinitesimal dx en el cuerpo sin deformar. Este segmento está orientado según una dirección determinada por el vector unitario n:
dx ≡ n dx;
|n| = 1;
|dx| = dx.
Tras el movimiento, el segmento acaba convertido en dx', cuyo módulo es dx':
dx' ≡ |dx|.
El estiramiento λ es un campo que indica lo que cambia la longitud del segmento infinitesimal en función de la dirección:
λ ≡ dx' ⁄ dx.
El estiramiento depende del punto en el que se mide y de la dirección. Es una medida de deformación ya que si hay cambio de longitud hay deformación, pero resulta bastante incómoda de utilizar.
Es fácil relacionar el estiramiento con el tensor de deformación de Cauchy-Green C. Sabemos lo siguiente:
(dx')2 = dxT ⋅ C ⋅ dx.
Es decir:
dx' = (dxT ⋅ C ⋅ dx)1 ⁄ 2.
Por otra parte, tenemos que
dx = n dx.
Por lo tanto,
dx' = (nT ⋅ C ⋅ n)1 ⁄ 2 dx.
De aquí extraemos la relación entre el estiramiento y el tensor de deformación de Cauchy-Green:
λ = dx' ⁄ dx = (nT ⋅ C ⋅ n)1 ⁄ 2.
Otra forma de verlo es que el cuadrado del estiramiento es una forma cuadrática en la dirección de medida:
λ2 = nT ⋅ C ⋅ n.
Categorías: Física
Permalink: http://sgcg.es/articulos/2017/09/26/deformaciones-mecanicas-8/
Nuevo récord de puntuación de Yuzuru Hanyu
2017-09-23
Yuzuru Hanyu ha vuelto a superar la mejor marca histórica en un programa corto de patinaje artístico sobre hielo en el Autumn Classic International de este año con la friolera de 112,72 puntos. Para hacernos a la idea de lo que es esto, vamos a evaluar el desglose de la puntuación conseguida con lo que podría lograr el mismo programa realizado a la perfección con ayuda de la escala de valores. Recordemos que en elementos técnicos, la puntuación es la suma de:
- la puntuación base del elemento (aumentada en una décima parte si se trata de un salto ejecutado en la segunda mitad del programa);
- un incremento por el grado de ejecución (GOE, de acuerdo con la tabla de la escala de valores);
- deducciones que contribuyen en negativo y que no hay en este caso.
La siguiente tabla muestra los elementos técnicos con valor base más GOE y el valor base más el GOE máximo posible:
| Elemento | Valor base + GOE | Valor base + GOE máximo |
|---|---|---|
| 4S | 10,50+3,00 | 10,50+3,00 |
| FCSp4 | 3,20+1,10 | 3,20+1,50 |
| CSSp4 | 3,00+1,50 | 3,00+1,50 |
| 3A | 8,50⋅1,10+3,00 | 8,50⋅1,10+3,00 |
| 4T+3T | (10,30+4,30)⋅1,10+2,80 | (10,30+4,30)⋅1,10+3,00 |
| StSq4 | 3,90+1,96 | 3,90+2,10 |
| CCoSp4 | 3,50+1,30 | 3,50+1,50 |
| Total | 64,17 | 65,11 |
La otra contribución a la puntuación total, los componentes de programa, que en un programa corto masculino suma con factor unitario:
| Componente | Puntuación | Puntuación máxima |
|---|---|---|
| Skating Skills | 9,65 | 10,00 |
| Transitions | 9,55 | 10,00 |
| Performance | 9,80 | 10,00 |
| Composition | 9,80 | 10,00 |
| Interpretation of the Music | 9,75 | 10,00 |
| Total | 48,55 | 50,00 |
La puntuación total fue de 112,72. El mismo programa podría alcanzar 115,11 puntos si estuviera hecho a la perfección. Otra forma de verlo es que Yuzuru Hanyu estuvo a menos de 21 milésimas partes de hacer su programa perfectamente.
Categorías: Actualidad, Deporte
Permalink: http://sgcg.es/articulos/2017/09/23/nuevo-record-de-puntuacion-de-yuzuru-hanyu/
Deformaciones mecánicas (7)
2017-09-22
En general, los cuerpos y medios materiales no permanecen perfectamente quietos, sino que se mueven y cambian de forma según transcurre el tiempo como consecuencia de sus interacciones con el entorno y de su propia dinámica interna. Esta serie de artículos trata sobre los cambios de forma o deformaciones.
El tensor de deformación de Cauchy-Green
Vamos a usar la misma notación que en el artículo anterior. Volvemos a fijarnos en un segmento infinitesimal dx que, tras un movimiento, acaba convertido en el segmento infinitesimal dx'.

Deformación de un segmento infinitesimal.
El cuadrado de la longitud del segmento infinitesimal tras el movimiento es una forma cuadrática del cuadrado de la longitud del segmento infinitesimal antes del movimiento:
(dx')T ⋅ dx = dxT ⋅ [(∇x')T ⋅ ∇x'] ⋅ dx = dxT ⋅ C ⋅ dx.
El símbolo C denota al tensor de deformación de Cauchy-Green, cuya componente i,j-ésima en ejes cartesianos es
Cij ≡ ∑k(∂x'k ⁄ ∂xi) (∂x'k ⁄ ∂xj).
Como se aprecia, este tensor es simétrico.
El tensor de deformación de Cauchy-Green C está relacionado con el de Green-Lagrange ε. Recordemos que el tensor de deformación de Green-Lagrange sirve para construir una forma cuadrática que relaciona lo que cambia el cuadrado de la longitud del segmento infinitesimal con su valor inicial:
(dx')T ⋅ dx' − dxT ⋅ dx = dxT ⋅ (2 ε) ⋅ dx.
De esto se deduce la siguiente relación (en la que aparece el símbolo I como la matriz unidad):
ε = (1 ⁄ 2) (C − I).
Categorías: Física
Permalink: http://sgcg.es/articulos/2017/09/22/deformaciones-mecanicas-7/
La Electronic Frontier Foundation abandona el W3C ante la imposibilidad de frenar EME
2017-09-18
El World Wide Web Consortium, como se esperaba, ha publicado como recomendación el estándar EME, que establece una manera de que los navegadores web utilicen sistemas DRM para reproducir contenidos audiovisuales que son, se dice, defectuosos por diseño. Los sistemas DRM sirven para gestionar restricciones artificiales al uso de los contenidos y, por su naturaleza, se oponen a los intereses de los usuarios de los sistemas informáticos, que dejan de tener el dominio absoluto sobre su propiedad: un dispositivo que ejecuta un sistema DRM no obedece al usuario, sino a la empresa que puso dicho sistema. EME no estandariza ningún sistema DRM, pero sí la manera con la que dicho sistema interactúa con el navegador (digamos que secuestra el navegador), lo que sigue siendo una anticaracterística. Esto es tan absurdo como estandarizar un mecanismo para la difusión de virus informáticos: en ambos casos no se estandariza el programa que desobedece al usuario, pero sí la manera de que dicho programa pueda empezar a operar. La publicación de EME como recomendación legitima unos programas que atentan contra la web abierta y sirven para conspirar contra los intereses de los usuarios.
La Electronic Frontier Foundation, que lleva más de cuarto de siglo velando por los derechos civiles en el mundo de las telecomunicaciones, formaba parte del World Wide Web Consortium hasta ahora y luchó con todos los medios disponibles para evitar la publicación de EME o, al menos, mitigar sus posibles consecuencias nocivas. El proceso de elaboración y publicación de EME, en sí, estuvo marcado por todo menos por el consenso (tres quintos de los miembros votaron a favor de la publicación, lo que significa que dos quintos no la apoyaron). El proceso ha seguido adelante y sin compromiso a pesar de los múltiples problemas señalados por muchos miembros del consorcio. Como resultado de esta situación en la que una parte importante de los miembros del World Wide Web Consortium carece de la más mínima influencia ante una decisión que reconoce y aprueba el abandono de una web abierta y segura, la Electronic Frontier Foundation ha abandonado el consorcio.
Categorías: Actualidad, Derechos, Informática
Deformaciones mecánicas (6)
2017-09-17
En general, los cuerpos y medios materiales no permanecen perfectamente quietos, sino que se mueven y cambian de forma según transcurre el tiempo como consecuencia de sus interacciones con el entorno y de su propia dinámica interna. Esta serie de artículos trata sobre los cambios de forma o deformaciones.
El tensor de deformación de Green-Lagrange
Describimos, como en los anteriores artículos, un cuerpo material cuyos puntos están identificados por sus posiciones iniciales de radio vector x. El cuerpo experimenta un movimiento general en el que puede desplazarse sin más, pero también cambiar de forma, de manera que sus puntos acaban en posiciones
x'(x) ≡ x + u(x).
El campo u(x) es el campo de desplazamientos en formulación material o lagrangiana, es decir, referido a las posiciones iniciales de los puntos materiales, no a posiciones fijas en el espacio.
Fijémonos en un segmento infinitesimal dx en el instante inicial. Con el movimiento, el segmento se transforma en otro, dx'.

Deformación de un segmento infinitesimal.
Vamos a trabajar con representaciones matriciales en coordenadas cartesianas con cierto abuso de notación. Un vector columna x es una matriz columna cuyas componentes son las del vector homónimo en el sistema de referencia elegido. La traspuesta de esta matriz es un vector fila xT. Por su parte, los tensores de segundo orden tienen representaciones matriciales que son matrices cuadradas cuyas componentes son las de los propios tensores en el sistema de ejes elegido. La traspuesta de la representación matricial A de un tensor homónimo es la matriz AT, cuya componente i,j-ésima es la componente j,i-ésima de la representación matricial sin trasponer.
Seguimos buscando una medida eficaz de lo que se deforma un cuerpo. Ya nos fijamos en que los cambios de longitud son interesantes. Queremos que la deformación sea una medida con un buen comportamiento frente a cambios de sistema de referencia, así que ha de ser una magnitud tensorial. El vector que apunta de un extremo a otro del segmento infinitesimal inicial es una magnitud tensorial (un vector es un tensor de orden 1). El cuadrado de su longitud también es una magnitud tensorial (un escalar es un tensor de orden 0):
(dx)T ⋅ dx.
El cuadrado de la longitud final (tras el movimiento) del segmento infinitesimal es
(dx')T ⋅ dx'.
Sabemos que el segmento infinitesimal tras el movimiento está relacionado con el segmento infinitesimal en el estado inicial mediante una aplicación lineal (el diferencial):
dx' = dx + ∇u ⋅ dx.
De esto se extrae la siguiente expresión:
(dx')T ⋅ dx' = (dx)T ⋅ dx + (dx)T ⋅ [(∇u)T + ∇u +(∇u)T ⋅ ∇u] ⋅ dx.
La diferencia entre el cuadrado de la longitud final y el cuadrado de la longitud inicial queda como una forma cuadrática sobre la longitud inicial:
(dx')T ⋅ dx' − (dx)T ⋅ dx = (dx)T ⋅ [(∇u)T + ∇u +(∇u)T ⋅ ∇u] ⋅ dx ≡ (dx)T ⋅ (2 ε) ⋅ dx.
El símbolo ε de la anterior expresión, una magnitud tensorial de orden 2, es el tensor de deformación de Green-Lagrange, que está definido así:
ε ≡ (1 ⁄ 2) [(∇u)T + ∇u +(∇u)T ⋅ ∇u].
La componente i,j-ésima de este tensor es
εij ≡ (1 ⁄ 2) [(∂uj ⁄ ∂xi) + (∂ui ⁄ ∂xj) + ∑k(∂uk ⁄ ∂xj) (∂uk ⁄ ∂xi)].
Este tensor de deformación es muy conveniente, ya que tiene la interpretación geométrica inmediata que hemos visto y se deriva exclusivamente del tensor gradiente de desplazamiento. Esta conveniencia se ve un poco limitada debido al término cuadrático.
Categorías: Física
Permalink: http://sgcg.es/articulos/2017/09/17/deformaciones-mecanicas-6/
Deformaciones mecánicas (5)
2017-09-16
En general, los cuerpos y medios materiales no permanecen perfectamente quietos, sino que se mueven y cambian de forma según transcurre el tiempo como consecuencia de sus interacciones con el entorno y de su propia dinámica interna. Esta serie de artículos trata sobre los cambios de forma o deformaciones.
Los tensores de gradiente de deformación y desplazamiento como formas lineales para el cálculo de diferenciales
Hagamos una descripción lagrangiana de un cuerpo tras experimentar un movimiento. Los puntos materiales, caracterizados por sus posiciones iniciales x, se desplazan de acuerdo con el campo vectorial de desplazamientos u(x) hasta alcanzar las posiciones finales x':
x'(x) ≡ x + u(x).
Introdujimos recientemente los tensores de gradiente de desplazamiento ∇u y de gradiente de deformación ∇x'. Hagamos uso de ellos.

Deformación de un segmento infinitesimal.
Elijamos un segmento infinitesimal du en la configuración inicial del cuerpo. Tras el movimiento, el segmento se convierte en
dx' = ∇x' ⋅ dx = dx + ∇u ⋅ dx = dx + du.
En componentes en ejes cartesianos, la expresión es la siguiente:
dx'i = ∑j(∂x'i ⁄ ∂xj) dxj = dxi + ∑j(∂ui ⁄ ∂xj) dxj = dxi + dui.
El primer sumando es el segmento infinitesimal inicial. El segundo sumando, más interesante, es lo que varía el desplazamiento entre ambos extremos del segmento infinitesimal. El gradiente de deformación proporciona una forma lineal que pasa de segmentos infinitesimales antes del movimiento a segmentos infinitesimales después del movimiento. El gradiente de desplazamientos proporciona una forma lineal que pasa de segmentos infinitesimales antes del movimiento a variaciones infinitesimales en los desplazamientos. Todo esto, por supuesto, es válido cuando el campo de desplazamientos (o la aplicación de posición inicial a posición final) es diferenciable.

Concepto de variación infinitesimal del desplazamiento.
Categorías: Física
Permalink: http://sgcg.es/articulos/2017/09/16/deformaciones-mecanicas-5/
Deformaciones mecánicas (4)
2017-09-14
En general, los cuerpos y medios materiales no permanecen perfectamente quietos, sino que se mueven y cambian de forma según transcurre el tiempo como consecuencia de sus interacciones con el entorno y de su propia dinámica interna. Esta serie de artículos trata sobre los cambios de forma o deformaciones.
El tensor de gradiente deformación
Hagamos una descripción lagrangiana de un cuerpo tras experimentar un movimiento. Los puntos materiales, caracterizados por sus posiciones iniciales x, se desplazan de acuerdo con el campo vectorial de desplazamientos u(x) hasta alcanzar las posiciones finales x':
x'(x) ≡ x + u(x).
El tensor de gradiente de deformación es el gradiente de este campo de posiciones finales:
∇x'(x).
El tensor de gradiente de deformación es similar al tensor lagrangiano de gradiente de desplazamiento. La componente i,j-ésima del tensor de gradiente de deformación está relacionada con la correspondiente del tensor de gradiente de desplazamiento; esta relación es especialmente simple en ejes cartesianos:
∂x'i ⁄ ∂xj = δij + ∂ui ⁄ ∂xj.
En la anterior expresión, δij es 1 cuando i = j y 0 en el resto de los casos.
Categorías: Física
Permalink: http://sgcg.es/articulos/2017/09/14/deformaciones-mecanicas-4/
El problemático artículo 13 de la directiva del Parlamento Europeo y del Consejo sobre los derechos de autor en el mercado único digital
2017-09-12
La directiva del Parlamento Europeo y del Consejo sobre los derechos de autor en el mercado único digital, que está bajo revisión, requiere en su artículo 13 que los proveedores de servicios de la sociedad de la información que almacenen y faciliten el acceso público a grandes cantidades de obras subidas por los usuarios implanten medidas de vigilancia y reconocimiento de contenidos para asegurar para asegurar que el material subido está en regla en materia de derechos de autor. Esto es problemático por múltiples motivos:
- los sistemas de filtrado son imperfectos y a menudo provocan la eliminación de contenido que está en regla;
- la implantación de estos sistemas no supone un gran obstáculo para las empresas grandes bien establecidas, pero sí puede tener un coste prohbitivo para nuevas empresas y otras organizaciones pequeñas;
- la carga de la prueba cae sobre quien sube el contenido, que es culpable de violar los derechos de autor sin más que así lo dicte una máquina y ha de demostrar su inocencia;
- los filtros automáticos están muy lejos de detectar las excepciones legales que existen a las restricciones de los derechos de autor.
Categorías: Actualidad, Derechos
Deformaciones mecánicas (3)
2017-09-06
En general, los cuerpos y medios materiales no permanecen perfectamente quietos, sino que se mueven y cambian de forma según transcurre el tiempo como consecuencia de sus interacciones con el entorno y de su propia dinámica interna. Esta serie de artículos trata sobre los cambios de forma o deformaciones.
El tensor de gradiente de desplazamiento
El campo de desplazamientos propociona una descripción cinemática completa de lo que le sucede a un cuerpo que se deforma, pero la información es demasiado cruda: ¿cómo podemos distinguir los movimientos de sólido rígido de las deformaciones? Puede ser conveniente ir paso a paso y librarnos inicialmente de un tipo muy concreto de movimiento de sólido rígido: la traslación. En una traslación pura, todos los puntos se desplazan igual: según una descripción lagrangiana (en la que seguimos cada punto del cuerpo en su movimiento y etiquetamos cada punto con las coordenadas de su posición inicial), el campo de desplazamientos es uniforme, es decir, no varía de un punto a otro. Esto sugiere que una buena descripción de la deformación podría estar relacionada de alguna manera con cómo varía el vector desplazamiento de un punto a otro, pues si no hay variación, tenemos una traslación pura, sin deformación. Tomemos en un cierto instante de tiempo un campo vectorial de desplazamiento u(x) en función del vector de posición x. Si la descripción es lagrangiana, el vector de posición es el del punto material en su posición inicial, mientras que si la descripción es euleriana, el vector de posición es el del punto espacial en el que se mide en el instante final. Una buena manera de expresar la variación del vector de desplazamientos con la posición inicial es el gradiente:
∇u(x).
Definamos un sistema de coordenadas cartesianas con ejes designados con los índices 1, 2 y 3. El vector de posición tiene como componente en el eje i-ésimo el valor xi y el vector de desplazamiento tiene como componente en el eje i-ésimo el valor ui. El gradiente de desplazamientos, que es un tensor de orden 2, tiene por componente i,j-ésima la expresión
∂ui ⁄ ∂xj.
Esta expresión es así de sencilla en coordenadas cartesianas. En un sistema curvilíneo (entre los que destacan las coordenadas cilíndricas y las esféricas), el álgebra se complica un poco.
Si la descripción es lagrangiana y las coordenadas son las de los puntos materiales en sus posiciones iniciales, el tensor es el tensor material de gradiente de desplazamientos. Si la descripción es euleriana y las coordenadas son las de los puntos espaciales en los que se mide en el instante final, el tensor es el tensor espacial de gradiente de desplazamientos.
Las traslaciones puras de sólido rígido dan como resultado un campo tensorial de gradiente de desplazamientos nulo. Las rotaciones puras y las deformaciones dan lugar a campos no nulos, pero veremos que es posible distinguir unos movimientos de otros.
Categorías: Física
Permalink: http://sgcg.es/articulos/2017/09/06/deformaciones-mecanicas-3/
