Junio de 2020
Calendario de artículos de de 2020
| lu | ma | mi | ju | vi | sá | do |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | |||||
Flores (7)
2020-06-28
He aquí una fotografía de una flor tomada con una lente con mucha aberración esférica que provoca un efecto resplandeciente, etéreo.

Fotografía de una flor tomada con una lente con mucha aberración
esférica. Más
grande.
Categorías: Fotografía
Flores (6)
2020-06-27
He aquí una fotografía de una flor tomada con una lente con mucha aberración esférica que provoca un efecto resplandeciente, etéreo.

Fotografía de una flor tomada con una lente con mucha aberración
esférica. Más
grande.
Categorías: Fotografía
Flores (5)
2020-06-26
He aquí una fotografía de una flor tomada con una lente con mucha aberración esférica que provoca un efecto resplandeciente, etéreo.

Fotografía de una flor tomada con una lente con mucha aberración
esférica. Más
grande.
Categorías: Fotografía
Flores (4)
2020-06-23
He aquí una fotografía de una flor tomada con una lente con mucha aberración esférica que provoca un efecto resplandeciente, etéreo.

Fotografía de una flor tomada con una lente con mucha aberración
esférica. Más
grande.
Categorías: Fotografía
Flores (3)
2020-06-22
He aquí una fotografía de una flor tomada con una lente con mucha aberración esférica que provoca un efecto resplandeciente, etéreo.

Fotografía de una flor tomada con una lente con mucha aberración
esférica. Más
grande.
Categorías: Fotografía
Flores (2)
2020-06-20
He aquí una fotografía de una flor tomada con una lente con mucha aberración esférica que provoca un efecto resplandeciente, etéreo.

Fotografía de una flor tomada con una lente con mucha aberración
esférica. Más
grande.
Categorías: Fotografía
Flores (1)
2020-06-19
He aquí una fotografía de una flor tomada con una lente con mucha aberración esférica que provoca un efecto resplandeciente, etéreo.

Fotografía de una flor tomada con una lente con mucha aberración
esférica. Más
grande.
Categorías: Fotografía
Repuntes y no repuntes
2020-06-17
Estamos en medio de una espeluznante epidemia y, comprensiblemente, los medios de comunicación buscan noticias relacionadas con esta situación. Surge un problema cuando lo que afirman las noticias no está respaldado por los datos en los que supuestamente se basan. ¿Quién no ha leído sobre numerosos repuntes del número de muertes, del número de contagios… en España durante estos meses? Esto, siempre basándose en los datos oficiales. Luego resultaba que esos supuestos repuntes no eran más que un día con un número mayor que el número del día anterior, pero no más allá de las variaciones normales de los mismos datos oficiales que supuestamente justificaban la noticia. ¿Acaso no es difícil afirmar que se produce un repunte usando el dato puntual de un solo día? En una epidemia, un repunte ha de ser un cambio de tendencia al alza y la tendencia no se establece con un único dato. Como muestra de ello, veamos esta gráfica de nuevos casos de COVID-19 incorporados cada día a la serie de datos publicada por la Comunidad de Madrid:
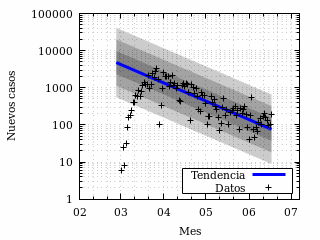
Evolución de los nuevos casos diarios de una epidemia.
Las áreas sombreadas, por amplitud creciente, abarcan una desviación
típica por encima y por debajo de la tendencia, dos desviaciones
típicas por encima y por debajo de la tendencia y tres desviaciones
típicas por encima y por debajo de la tendencia.
¡No es difícil encontrar aumentos puntuales diarios de un orden de magnitud en los nuevos casos! Aun así, la tendencia de descenso de aproximadamente un 4 % diario se mantiene bastante imperturbable desde finales de marzo. Algo similar ha sucedido en muchos otros territorios, tanto con los nuevos casos como con los fallecimientos. Simplemente basándonos en una serie temporal con este aspecto, no es legítimo hablar de repuntes basándonos en cualquier máximo local. Si de pronto los datos se explican mucho mejor con un cambio de tendencia al alza (que podría suceder en un futuro próximo y también podría no suceder en un futuro próximo) que con la hipótesis nula de que la tendencia permanece a la baja, entonces podrá hablarse de un repunte, pero para ello hacen falta bien muchos días con números moderadamente elevados, bien pocos días con números aterradoramente elevados. Veremos durante las próximas semanas cuándo sucede esto.
En muchas circunstancias, los modelos epidemiológicos elementales predicen comportamientos exponenciales durante las fases de crecimiento inicial y de decaimiento final. Esto es consecuencia natural de poder modelar, aunque sea aproximadamente, la dinámica de la epidemia de una forma que se deja linealizar. Si nuestro modelo mental de tendencia es así, las tendencias y las desviaciones relativas a ellas se ven bien en escala logarítmica.
Categorías: Salud
Permalink: http://sgcg.es/articulos/2020/06/17/repuntes-y-no-repuntes/
El modelo epidemiológico SIR (20)
2020-06-16
El modelo SIR es un modelo muy sencillo del comportamiento de una epidemia a lo largo del tiempo. Tras explicar algunas características del modelo, vimos:
- cómo simplificar el modelo para analizar el comienzo de la propagación de una nueva epidemia;
- el comportamiento de la proporción de infectados en esta fase inicial;
- cómo relacionar las variables sin necesidad de integrar en el tiempo;
- cómo calcular el máximo número de infectados simultáneos;
- cómo calcular el resultado final de la epidemia;
- cómo se comporta la epidemia en el entorno del máximo de infectados simultáneos;
- cómo varían los infectados cerca del final de la epidemia;
- cómo se relacionan la fase de crecimiento exponencial inicial de la epidemia y la fase de decrecimiento exponencial final de la epidemia;
- qué condición es necesaria para la inmunidad de grupo;
- cómo queda modificado el modelo si en vez de trabajar con proporciones sobre la población total, trabajamos con números absolutos de individuos;
- cómo plantear el modelo cuando hay nacimientos y defunciones, pero la población total se mantiene estable;
- cómo extraer el ritmo reproductivo básico del modelo con natalidad y mortalidad en equilibrio;
- los puntos fijos o puntos de equilibrio del sistema referido a los susceptibles y los infectados;
- la naturaleza del punto de equilibrio libre de enfermedad;
- la naturaleza del equilibrio endémico;
- cómo las soluciones se mantienen confinadas en el conjunto de valores que tiene sentido físico;
- cómo las soluciones siempre convergen a algún punto de equilibrio (bien el equilibrio endémico, bien el equilibrio libre de enfermedad).
- un repaso gráfico al comportamiento del sistema para varios conjuntos de parámetros.
Hoy vamos a ilustrar cómo varían las soluciones en función de si el equilibrio endémico es un nodo atractor o una espiral.
Recordemos que estamos estudiando el siguiente sistema autónomo:
dS ⁄ dt = μ − (1+μ) R0 S I − μ S;
dI ⁄ dt = (1+μ) R0 S I − (1+μ) I.
Aparecen varios símbolos cuyo significado es el siguiente:
- La variable dependiente S es la proporción susceptible de la población total.
- La variable dependiente I es la proporción de la población infectada.
- La variable independiente t es el tiempo hecho adimensional de forma que la población infectada pasa a ser población recuperada a un ritmo por unidad de tiempo adimensional igual a la propia población infectada. El primer artículo sobre los puntos fijos explica esto.
- El símbolo μ denota tanto la natalidad como la mortalidad, que son iguales. Este número es nulo en el caso en el que no hay nacimientos ni muertes (o cuando se producen a un ritmo tan lento que es legítimo despreciar su efecto) y es positivo en el caso más general.
- El símbolo R0 es el ritmo reproductivo básico (los nuevos contagios que provoca el caso inicial). Este número es nulo en el caso trivial de una enfermedad que no se contagia y positivo en el caso general de las enfermedades contagiosas.
Vimos en el último artículo los retratos de fase correspondientes a varios parámetros. Estos retratos de fase ilustran muy bien las soluciones de forma global, pero no está de más echar un vistazo a la evolución temporal de algunas soluciones particulares.
Nodo como equilibrio endémico
La siguiente figura muestra la diferencia entre una evolución particular de una epidemia endiabladamente intensa cuando la natalidad es nula y cuando hay una natalidad pequeña. Las curvas de infectados activos se siguen durante un tiempo hasta que se impone el comportamiento a largo plazo de convergencia exponencial al nodo que es el equilibrio endémico en el caso con natalidad.
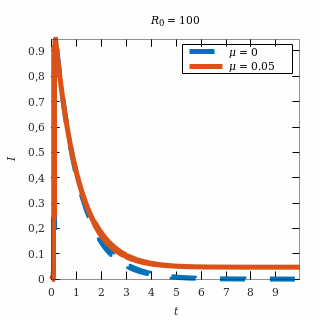
Solución particular de una epidemia con un nodo como equilibrio
endémico comparada con la misma epidemia cuando no hay natalidad.
Espiral como equilibrio endémico
La siguiente figura muestra la diferencia entre una evolución particular de una epidemia cuando la natalidad es nula y cuando hay una natalidad pequeña. Las curvas de infectados activos se siguen durante un tiempo hasta que se impone el comportamiento a largo plazo de convergencia oscilatoria a la espiral que es el equilibrio endémico en el caso con natalidad.
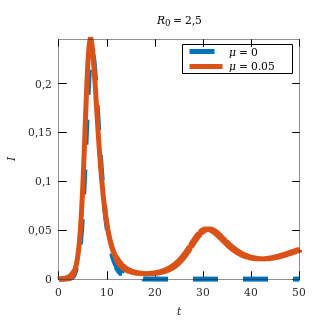
Solución particular de una epidemia con una espiral como
equilibrio endémico comparada con la misma epidemia cuando no hay
natalidad.
Categorías: Matemáticas, Salud
Permalink: http://sgcg.es/articulos/2020/06/16/el-modelo-epidemiologico-sir-20/
El modelo epidemiológico SIR (19)
2020-06-13
El modelo SIR es un modelo muy sencillo del comportamiento de una epidemia a lo largo del tiempo. Tras explicar algunas características del modelo, vimos:
- cómo simplificar el modelo para analizar el comienzo de la propagación de una nueva epidemia;
- el comportamiento de la proporción de infectados en esta fase inicial;
- cómo relacionar las variables sin necesidad de integrar en el tiempo;
- cómo calcular el máximo número de infectados simultáneos;
- cómo calcular el resultado final de la epidemia;
- cómo se comporta la epidemia en el entorno del máximo de infectados simultáneos;
- cómo varían los infectados cerca del final de la epidemia;
- cómo se relacionan la fase de crecimiento exponencial inicial de la epidemia y la fase de decrecimiento exponencial final de la epidemia;
- qué condición es necesaria para la inmunidad de grupo;
- cómo queda modificado el modelo si en vez de trabajar con proporciones sobre la población total, trabajamos con números absolutos de individuos;
- cómo plantear el modelo cuando hay nacimientos y defunciones, pero la población total se mantiene estable;
- cómo extraer el ritmo reproductivo básico del modelo con natalidad y mortalidad en equilibrio;
- los puntos fijos o puntos de equilibrio del sistema referido a los susceptibles y los infectados;
- la naturaleza del punto de equilibrio libre de enfermedad;
- la naturaleza del equilibrio endémico;
- cómo las soluciones se mantienen confinadas en el conjunto de valores que tiene sentido físico;
- cómo las soluciones siempre convergen a algún punto de equilibrio (bien el equilibrio endémico, bien el equilibrio libre de enfermedad).
Hoy vamos a ilustrar el comportamiento del sistema para varios conjuntos de parámetros.
Recordemos que estamos estudiando el siguiente sistema autónomo:
dS ⁄ dt = μ − (1+μ) R0 S I − μ S;
dI ⁄ dt = (1+μ) R0 S I − (1+μ) I.
Aparecen varios símbolos cuyo significado es el siguiente:
- La variable dependiente S es la proporción susceptible de la población total.
- La variable dependiente I es la proporción de la población infectada.
- La variable independiente t es el tiempo hecho adimensional de forma que la población infectada pasa a ser población recuperada a un ritmo por unidad de tiempo adimensional igual a la propia población infectada. El primer artículo sobre los puntos fijos explica esto.
- El símbolo μ denota tanto la natalidad como la mortalidad, que son iguales. Este número es nulo en el caso en el que no hay nacimientos ni muertes (o cuando se producen a un ritmo tan lento que es legítimo despreciar su efecto) y es positivo en el caso más general.
- El símbolo R0 es el ritmo reproductivo básico (los nuevos contagios que provoca el caso inicial). Este número es nulo en el caso trivial de una enfermedad que no se contagia y positivo en el caso general de las enfermedades contagiosas.
Veamos unos cuantos retratos de fase, que muestran la forma de las trayectorias del sistema en el plano S, I.
En los retratos de fase siguientes, el equilibrio libre de enfermedad aparece como un símbolo vacío en S = 1, I = 0; el equilibrio endémico aparece como un símbolo relleno, las trayectorias son líneas continuas y las flechas indican la dirección del campo de velocidades dS ⁄ dt, dI ⁄ dt.
Las epidemias son débiles cuando 1 < R0 < (2 ⁄ μ) [1+μ−√(1+μ)] y el equilibrio endémico es un nodo estable; son moderadas cuando (2 ⁄ μ) [1+μ−√(1+μ)] < R0 < (2 ⁄ μ) [1+μ+√(1+μ)] y el equilibrio endémico es una espiral atractora; y son fuertes cuando R0 > (2 ⁄ μ) [1+μ+√(1+μ)] y el equilibrio endémico vuelve a ser un nodo estable.
Recordemos que estábamos expresando el tiempo en unidades tales que el ritmo de recuperación es unitario. La natalidad es baja cuando el ritmo de natalidad es muy inferior al ritmo de recuperación (μ ≪ 1) y la epidemia se comporta como si no hubiera natalidad durante mucho tiempo antes de que se note el efecto de la natalidad; la natalidad es moderada cuando el ritmo de natalidad es próximo al ritmo de recuperación (μ ≅ 1) y los efectos de natalidad y recuperación son comparables; y la natalidad es alta cuando el ritmo de natalidad es muy superior al ritmo de recuperación (μ ≫ 1) y el efecto de recuperación es despreciable.
Epidemia con natalidad nula
Con una natalidad nula (μ = 0) y una epidemia cualquiera (R0 > 1), no existe el equilibrio endémico y todas las trayectorias acaban en algún punto del eje I = 0.
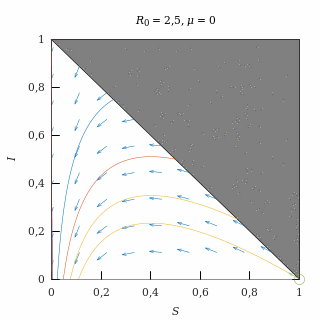
Retrato de fase de una epidemia con natalidad nula.
Epidemia débil con natalidad baja
Con una natalidad baja (μ = 0,05) y una epidemia débil (R0 = 1,01), el equilibrio endémico es un nodo estable, así que casi todas las trayectorias (salvo las del eje I = 0) acaban convergiendo exponencialmente al equilibrio endémico.
Como la natalidad es baja, las trayectorias permanecen durante mucho tiempo muy similares a las que se producen sin natalidad y, finalmente, quiebran para dirigirse hacia el equilibrio endémico.
El equilibrio endémico está muy próximo al equilibrio libre de enfermedad debido a que la epidemia es débil.
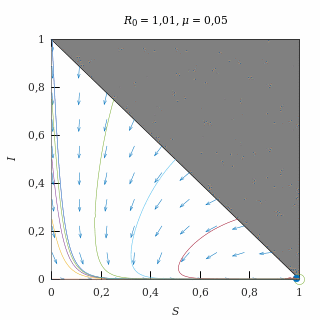
Retrato de fase de una epidemia débil con natalidad baja.
Epidemia moderada con natalidad baja
Con una natalidad baja (μ = 0,05) y una epidemia moderada (R0 = 2,5), el equilibrio endémico es una espiral atractora, así que casi todas las trayectorias (salvo las del eje I = 0) acaban convergiendo oscilatoriamente al equilibrio endémico.
Como la natalidad es baja, las trayectorias permanecen durante mucho tiempo muy similares a las que se producen sin natalidad y, finalmente, quiebran para dirigirse hacia el equilibrio endémico.
El equilibrio endémico está lejos del equilibrio libre de enfermedad debido a que la epidemia es moderada.
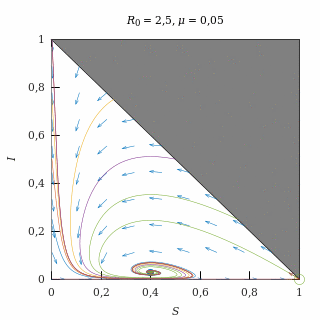
Retrato de fase de una epidemia moderada con natalidad baja.
Epidemia fuerte con natalidad baja
Con una natalidad baja (μ = 0,05) y una epidemia fuerte (R0 = 100), el equilibrio endémico es una espiral atractora, así que casi todas las trayectorias (salvo las del eje I = 0) acaban convergiendo oscilatoriamente al equilibrio endémico.
Como la natalidad es baja, las trayectorias permanecen durante mucho tiempo muy similares a las que se producen sin natalidad y, finalmente, quiebran para dirigirse hacia el equilibrio endémico.
El equilibrio endémico deja muy pocos susceptibles debido a que la epidemia es fuerte.
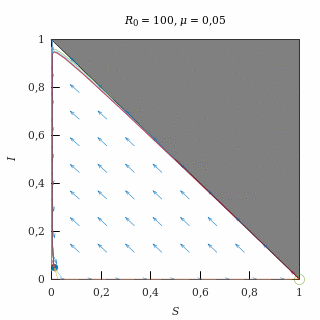
Retrato de fase de una epidemia fuerte con natalidad baja.
Epidemia débil con natalidad moderada
Con una natalidad moderada (μ = 1) y una epidemia débil (R0 = 1,15), el equilibrio endémico es un nodo estable, así que casi todas las trayectorias (salvo las del eje I = 0) acaban convergiendo exponencialmente al equilibrio endémico.
Como la natalidad es moderada, las trayectorias tienen poco que ver con las que se producían sin natalidad.
El equilibrio endémico está muy próximo al equilibrio libre de enfermedad debido a que la epidemia es débil.
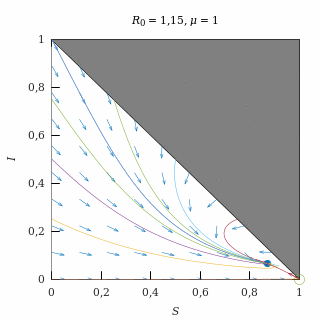
Retrato de fase de una epidemia débil con natalidad moderada.
Epidemia moderada con natalidad moderada
Con una natalidad moderada (μ = 1) y una epidemia moderada (R0 = 4), el equilibrio endémico es una espiral atractora, así que casi todas las trayectorias (salvo las del eje I = 0) acaban convergiendo oscilatoriamente al equilibrio endémico.
Como la natalidad es moderada, las trayectorias tienen poco que ver con las que se producían sin natalidad.
El equilibrio endémico está lejos del equilibrio libre de enfermedad debido a que la epidemia es moderada.
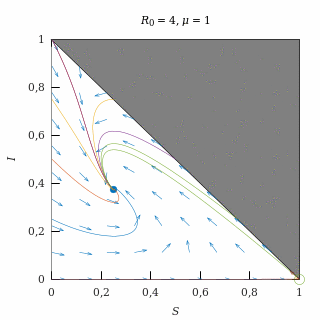
Retrato de fase de una epidemia moderada con natalidad moderada.
Epidemia fuerte con natalidad moderada
Con una natalidad moderada (μ = 1) y una epidemia fuerte (R0 = 10), el equilibrio endémico es un nodo estable, así que casi todas las trayectorias (salvo las del eje I = 0) acaban convergiendo exponencialmente al equilibrio endémico.
Como la natalidad es moderada, las trayectorias tienen poco que ver con las que se producían sin natalidad.
El equilibrio endémico deja muy pocos susceptibles debido a que la epidemia es fuerte.
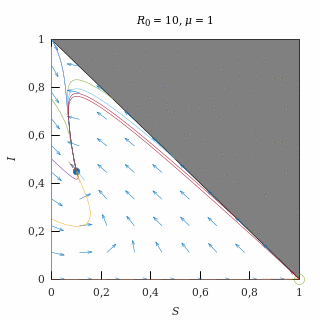
Retrato de fase de una epidemia fuerte con natalidad moderada.
Epidemia débil con natalidad alta
Con una natalidad alta (μ = 10) y una epidemia débil (R0 = 1,25), el equilibrio endémico es un nodo estable, así que casi todas las trayectorias (salvo las del eje I = 0) acaban convergiendo exponencialmente al equilibrio endémico.
Como la natalidad es alta, las trayectorias tienden a vivir en el eje S + I = 1, que es el que corresponde a una situación en la que no hay tasa de recuperación.
El equilibrio endémico está muy próximo al equilibrio libre de enfermedad debido a que la epidemia es débil.
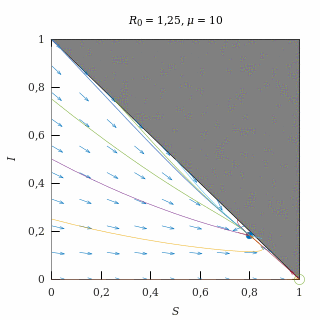
Retrato de fase de una epidemia débil con natalidad alta.
Epidemia moderada con natalidad alta
Con una natalidad alta (μ = 10) y una epidemia moderada (R0 = 2), el equilibrio endémico es una espiral atractora, así que casi todas las trayectorias (salvo las del eje I = 0) acaban convergiendo oscilatoriamente al equilibrio endémico.
Como la natalidad es alta, las trayectorias tienden a vivir en el eje S + I = 1, que es el que corresponde a una situación en la que no hay tasa de recuperación.
El equilibrio endémico está lejos del equilibrio libre de enfermedad debido a que la epidemia es moderada.
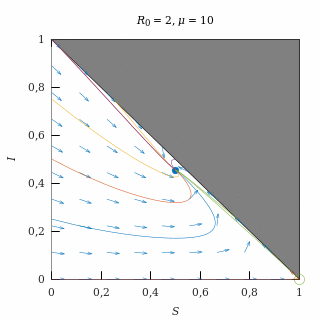
Retrato de fase de una epidemia moderada con natalidad moderada.
Epidemia fuerte con natalidad alta
Con una natalidad elevada (μ = 10) y una epidemia fuerte (R0 = 3,5), el equilibrio endémico es un nodo estable, así que casi todas las trayectorias (salvo las del eje I = 0) acaban convergiendo exponencialmente al equilibrio endémico.
Como la natalidad es alta, las trayectorias tienden a vivir en el eje S + I = 1, que es el que corresponde a una situación en la que no hay tasa de recuperación.
El equilibrio endémico deja muy pocos susceptibles debido a que la epidemia es fuerte.
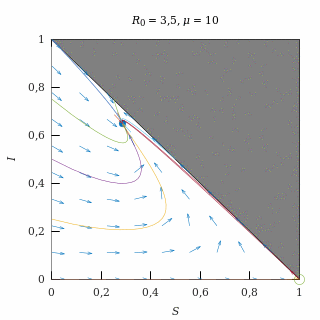
Retrato de fase de una epidemia fuerte con natalidad elevada.
Categorías: Matemáticas, Salud
Permalink: http://sgcg.es/articulos/2020/06/13/el-modelo-epidemiologico-sir-19/
La respirabilidad de las mascarillas está indicada de forma algo antinatural
2020-06-07
Las mascarillas quirúrgicas están sometidas a ensayos de respirabilidad de acuerdo con la norma EN 14683:2019+AC:2019. De acuerdo con esta norma, la respirabilidad está medida en Pa ⁄ cm2, es decir, en presión por unidad de superficie. Esta medida es muy extraña. ¿A qué se debe esto?
Cómo podríamos definir la respirabilidad
Al respirar, los pulmones se contraen y se expanden. Esta expansión y contracción requiere un esfuerzo muscular: el esfuerzo respiratorio. La musculatura respiratoria ha de vencer el salto de presión entre el interior de los pulmones y el exterior del cuerpo, así que el esfuerzo respiratorio crece conforme aumenta la magnitud del salto de presión. Por lo tanto, podemos caracterizar el esfuerzo respiratorio mediante la magnitud de la diferencia de presión ∆p entre el interior de los pulmones y el exterior.
Si se varía el caudal Q de aire respirado y se mantienen las demás condiciones constantes, el esfuerzo respiratorio varía: a más caudal, más esfuerzo requerido. El caudal satisface una necesidad fisiológica y el salto de presión es el esfuerzo necesario para satisfacer dicha necesidad. Una medida de la dificultad respiratoria puede ser, por lo tanto, el salto de presión dividido por el caudal de aire respirado:
∆p ⁄ Q.
Si el salto de presión es grande y el caudal respirado es pequeño, respirar es sin duda difícil.
La medida inversa, la facilidad respiratoria, podría ser el cociente del caudal respirado entre el salto de presión:
Q ⁄ ∆p.
Si se respira mucho caudal con poco salto de presión, respirar es fácil.
Respirar a través de una mascarilla puede ser en principio más difícil que respirar libremente. La presencia de la mascarilla obstaculiza el movimiento del aire y obliga a realizar un esfuerzo mayor que el normal al respirar. El aire que se filtra a través de la mascarilla experimenta una pérdida de presión que puede ser aproximada gracias a la ley de Darcy, que indica que el caudal respirado es proporcional al producto de la superficie A a través de la que se filtra el aire y el salto de presión:
Q = k A ∆p.
En esta ecuación, k es una constante que depende principalmente del material (su porosidad…) y la geometría detallada de la mascarilla (su espesor…), y, secundariamente, de otras cuestiones como la temperatura y la humedad del aire.
Una medida de facilidad respiratoria y, por lo tanto, de respirabilidad de una mascarilla, podría ser el cociente del caudal respirado (numerador) y el producto de la superficie a través de la que se filtra el aire y el salto de presión (denominador):
Q ⁄ (A ∆p) = k.
Un número elevado indicaría una mascarilla con buena respirabilidad en la que se consigue mucho caudal con poco salto de presión y poca superficie útil. Es interesante incluir la superficie en la medida, ya que permite estimar cómo varían los números con tallas diferentes antes de realizar ensayos empíricos de respirabilidad.
La superficie útil de la mascarilla es fija para una combinación de modelo de mascarilla y rostro del usuario. Si no interesa saber qué sucede con tamaños diferentes, otra medida adecuada de respirabilidad puede ser la anterior si se omite el factor de superficie:
Q ⁄ ∆p.
Qué dice la norma
El ensayo de respirabilidad consiste, de forma resumida, en interrumpir la sección transversal de un conducto con un recorte de la mascarilla mientras se fuerza cierto caudal de aire. Como la corriente ha de atravesar el recorte, se produce una pérdida de carga; la medida de respirabilidad es la pérdida de presión que se produce al pasar de aguas arriba del recorte a aguas abajo del recorte dividida entre la sección transversal del conducto. Con los símbolos anteriores, la respirabilidad que define la norma tiene la siguiente expresión:
∆p ⁄ A.
Las condiciones del aire son siempre las mismas, el caudal que hay que alcanzar es siempre el mismo y la sección transversal que hay que usar es siempre la misma, así que lo único que varía en función de la muestra de mascarilla es el salto de presión. Dar la presión diferencial divida por la sección transversal es, por lo tanto, equivalente a dar cualquier otro múltiplo cualquiera de la presión diferencial; como el factor multiplicativo es fijo, las medidas son comparables.
Dividir la presión diferencial entre la superficie no aporta nada. Como hemos visto anteriormente, la física hace que sea interesante, como mucho, el producto de la superficie y la presión, nunca el cociente de ambas magnitudes. Dar el cociente permitiría hacer trampas si fuera posible hacer ensayos con secciones de diferentes tamaños, pero la norma especifica una sección fija, afortunadamente, así que el cociente tiene el único efecto de expresar los resultados en unas unidades poco naturales.
Categorías: Física
