Julio de 2013
Calendario de artículos de de 2013
| lu | ma | mi | ju | vi | sá | do |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 | ||||
La botella y la bodega de avión (8)
2013-07-31
Continuamos con los artículos sobre lo que pasaría con una botella cerrada y llena de algún líquido al transportarla en la bodega de un avión. Vimos que el principal problema es aguantar el salto de presión entre el ambiente de la bodega (inferior a la que hay en tierra porque la presurización es limitada) y la del interior de la botella (similar a la que había al cerrarla en tierra). Esta diferencia de presión puede estar en el entorno de los 25 kPa.
Estamos diseñando un experimento para emular el efecto de la diferencia de presión en vuelo sobre el tapón de la botella. El experimento consiste en frenar repentinamente la botella para que su contenido se agolpe contra el tapón. Ayer hicimos un primer planteamiento que no funcionaba bien por los materiales disponibles. El experimento que planteamos hoy es muy satisfactorio por ser fácil y barato y permitir un control bastante decente de la aceleración de frenada.
Segundo intento de diseño de un sistema de frenado
Volvemos a usar una cuerda de tender de polipropileno tan larga como la altura de la caída, pero esta vez no fija rígidamente al techo, sino atada a un listón de abeto rojo.
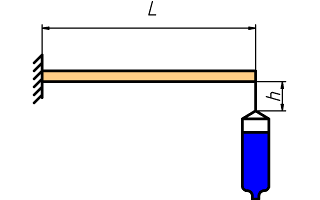
Dispositivo experimental: un listón de madera anclado a un banco
de trabajo y con la cuerda atada a un extremo.
El experimento consiste en dejar la botella a la altura del listón (es decir, con la cuerda sin extender) y dejarla caer repentinamente. La botella ha de frenar en vertical, así que hay que soltarla bien centrada bajo el punto de atadura de la cuerda al listón.
Hagamos un pequeño paréntesis para estudiar la cuerda. Como vimos en el artículo del pasado domingo, con una botella de dos litros, nuestro objetivo es alcanzar una carga de inercia (la suma de la aceleración experimentada por la botella y la aceleración gravitatoria) de unos 100 m s−2. Como la masa es de unos 2,0 kg, la fuerza que ha de aguantar la cuerda es de unos 200 N. Esta fuerza dividida por el área de la sección ha de superar la resistencia del material, que puede ser tan baja como 12 MPa. El valor mínimo del diámetro en estas condiciones está entre 4 mm y 5 mm; como las cuerdas vienen con diámetros en milímetros enteros, hay que conseguir una de al menos 5 mm. Si ancláramos rígidamente una cuerda de esta sección al techo, la aceleración conseguida no sería la de diseño, sino más del quíntuple, así que se rompería; es evidente que hace falta un anclaje apreciablemente flexible.
Vamos de vuelta al listón de madera. Este listón está anclado rígidamente en un extremo y tiene atada la botella en un punto alejado una distancia L. El listón tiene una sección rectángular de ancho b = 20 mm y altura t = 40 mm. La sección del listón tiene un segundo momento de área I = (1 ⁄ 12) b t3 ≈ 11 cm4; esta propiedad es importante en los cálculos porque guía el comportamiento a flexión. Ahora hay que saber las propiedades mecánicas. El material es abeto rojo, cuyo módulo elástico es E = 11 GPa y cuya resistencia es σu = 70 MPa.
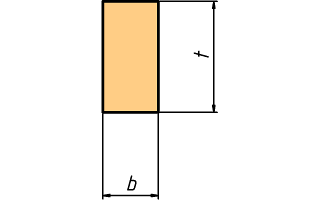
Sección transversal del listón.
Asumiremos que el listón se comporta como si no tuviera masa; es fácil comprobar que su inercia es pequeña en comparación con la de la botella.
El listón es mucho más flexible a flexión que la cuerda a tracción; como la cuerda cuelga del listón, toda la rigidez la aporta el último. La rigidez, que es la relación entre la carga que colgamos del listón y lo que esta carga desciende debido a que el listón se flexiona, es K = 3 E I ⁄ L3.
La masa es la misma que ayer y el sistema, cuando la botella llega abajo y tensa la cuerda, vibra igualmente con una frecuencia angular ω = (K ⁄ M)1 ⁄ 2. Esta vez, debido a la mayor flexibilidad (menor rigidez K), la frecuencia será mucho más baja.
Ayer vimos que la aceleración máxima de la botella cuando la rapidez de descenso justo antes de frenar es v y la aceleración gravitatoria es g0 ≈ 9,8 m s−2 es a = g0 [v ω ⁄ g0 + 1]1 ⁄ 2. La suma de esta aceleración y la gravitatoria es el valor objetivo a + g0 = 100 m s−2 necesario para que la sobrepresión en el tapón de la botella de dos litros alcance el valor deseado de unos 25 kPa. Podemos despejar el factor de carga objetivo n = v ω ⁄ g0, que en este caso ha de ser n = 8,9.
La tensión crítica σ a
la que está sometido el listón se da en las fibras más alejadas del
centro en el empotramiento. Esta tensión está relacionada con el
momento flector l P
de la carga máxima P =
M (a + g0 =
200 N mediante la expresión
σ =
L P t ⁄ (2 I).
Esta tensión ha de ser inferior a la resistencia del material σu para
que el listón no se rompa. De esto sale la siguiente restricción para
el brazo L:
L <
2 σu I ⁄ (P t).
Nos sale un brazo máximo muy largo: L
< 190 cm. Conviene que no nos aproximemos a la
resistencia del material; un brazo L
= 80 cm nos da una tensión máxima de 30 MPa, lo que es un buen margen.
La rapidez de la botella tras una caída desde una altura
h es v =
(2 g0 h)1 ⁄ 2.
Con esto y la frecuencia angular ω y el factor de carga n en función de las propiedades de las que
dependen, sale esta relación entre la altura de la caída (o longitud
de la cuerda) h y la distancia L de la cuerda al emptramiento (es decir,
el brazo):
h =
[n2 M g0 ⁄ (6 E I)] L3.
Si el brazo es L = 80 cm,
entonces sale una altura de suelta h = 11 cm. Estas dimensiones son muy
cómodas de manejar en un banco de trabajo en el que fijar el listón.
De propina: verificación de las simplificaciones de los cálculos
Entre los incautos lectores de esta página, hay algún ingeniero que aprecia estas cosas.
Dijimos que la inercia del listón es pequeña. Esto es fácil de comprobar. Si aplicamos una carga P en el extremo del listón de longitud L, la flecha allí es igual a L3 P ⁄ (3 E I) y la energía cinética máxima al oscilar a frecuencia angular ω es (1 ⁄ 2) ω2 M L6 P2 ⁄ (9 E2 I2). Si asumimos que la elástica del listón es casi la que sale a carga estática (que es la que usamos para calcular la deflexión en el extremo cargado), entonces la energía cinética máxima del listón sale de integrar la energía cinética de cada sección a lo largo de toda la longitud; el resultado es (1 ⁄ 2) ω2 11 ρ b t L7 P2 ⁄ (420 E2 I2). Lo único nuevo aquí es la densidad del material, 450 kg m−3. La energía cinética del listón dividida por la energía cinética de la botella es 33 ρ b t L ⁄ (140 M), es decir, como un 24 % de la masa del listón dividida entre la masa de la botella. La inercia del listón es un 3,4 % de la inercia de la botella y la frecuencia angular del sistema sería la correspondiente a sustituir la masa de la botella por ella misma incrementada en este 3,4 %, lo que supone reducir la frecuencia angular en un 1,7 %, algo muy pequeño, insignificante para nuestros fines.
También dijimos que la cuerda no aporta flexibilidad al sistema porque es tan inextensible que es como si la botella estuviera unida rígidamente al listón en el momento de alcanzar el punto de frenada. En efecto, para una carga P, la extensión de la cuerda es 4 h P ⁄ (Ecuerda π D2 = 4,3 μm N−1 P con Ecuerda = 1,3 GPa el módulo elástico de la cuerda. En cambio, la deflexión del extremo cargado del listón es 150 μm N−1 P, con lo que tener en cuenta la flexibilidad de la cuerda apenas supone un desplazamiento adicional del 3,0 %. Para calcular la frecuencia, sumaríamos las flexibilidades y sacaríamos el inverso de dicha suma para calcular la rigidez del sistema. Como la corrección es pequeña, el aumento del 3,0 % de la flexibilidad casi se corresponde con un descenso del 3,0 % de la rigidez y un descenso del 1,5 % de la frecuencia propia. El efecto combinado de esto y la inercia del listón supondría un descenso del 2,2 % en la frecuencia de oscilación. Ni la masa de la botella llena de líquido está determinada con tanta precisión, ni estamos valorando la inercia de la cuerda, ni estamos valorando la inercia del arnés que une la botella a la cuerda, ni estamos valorando muchos otros efectos, así que no tiene sentido refinar hasta este punto.
Otros artículos de la serie
- Introducción.
- Resistencia de la pared.
- Estabilidad de un tapón de corcho.
- Planteamiento general de un experimento para medir la capacidad del tapón.
- Experimento para medir la capacidad del tapón: caso de frenada instantánea.
- Experimento para medir la capacidad del tapón: caso de frenada gradual.
- Primer diseño del experimento.
Categorías: Física
Permalink: http://sgcg.es/articulos/2013/07/31/la-botella-y-la-bodega-de-avion-8/
La botella y la bodega de avión (7)
2013-07-30
Continuamos con los artículos sobre lo que pasaría con una botella cerrada y llena de algún líquido al transportarla en la bodega de un avión. Vimos que el principal problema es aguantar el salto de presión entre el ambiente de la bodega (inferior a la que hay en tierra porque la presurización es limitada) y la del interior de la botella (similar a la que había al cerrarla en tierra). Esta diferencia de presión puede estar en el entorno de los 25 kPa.
Estamos diseñando un experimento para emular el efecto de la diferencia de presión en vuelo sobre el tapón de la botella. El experimento consiste en frenar repentinamente la botella para que su contenido se agolpe contra el tapón. Ya vimos que detener la caída de la botella muy rápidamente provocaría sobrepresiones muy, muy grandes (aunque el caso límite estudiado es francamente difícil de poner en práctica). También vimos el otro extremo, el de una frenada suave y lenta (tal que la propagación de ondas acústicas es comparativamente instantánea), que es algo mucho más fácil de conseguir en la práctica y que ya provoca la sobrepresión buscada sin problemas. Hoy vamos a hacer una primera aproximación al frenado controlado de la botella, pero nos saldrá algo excesivamente brusco. Por supuesto, en vez del experimento que planteamos, podríamos dejar caer la botella y frenarla con las manos, pero eso sería mucho menos entretenido.
Primer intento de diseño de un sistema de frenado
Podemos frenar la caída con mediante una cuerda de tender de polipropileno tan larga como la altura de la caída. La cuerda frena la botella antes de que llegue al suelo. Lo que hacemos es montar un arnés alrededor del cuello de la botella de modo que este arnés permite una sujeción simétrica mediante la cuerda; la figura siguiente ilustra el concepto.
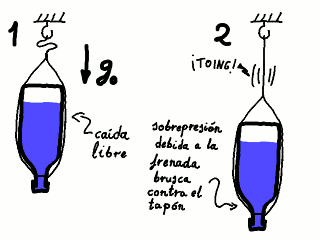
Primera disposición experimental para provocar una sobrepresión.
La longitud de la cuerda, h más adelante,
es igual a la altura de la caída.
La cuerda está atada rígidamente al techo. De esta manera, la única flexibilidad importante se debe a la cuerda, no a su anclaje.
Una cuerda de polipropileno típica tiene un módulo elástico efectivo E = 1,3 GPa, mientras que su resistencia a la tracción varía según el fabricante; encuentro tensiones de rotura entre σu = 12 MPa y σu = 25 MPa. Usaremos la resistencia más baja para dimensionar el sistema.
La cuerda, que es mucho más ligera que la botella llena de líquido
(cuya masa ronda M = 2 kg), se comporta
como un muelle cuya constante es
K =
E π D2 ⁄ (4 h),
donde D es el diámetro de la sección
transversal y h es la longitud de
la cuerda, que es lo mismo que la altura de la caída.
La cuerda actúa como muelle en el momento en el se extiende
por completo al llegar la botella abajo. Tenemos una masa
M (la masa de la botella
rellena y el arnés) sujeta a un muelle de constante K. Esto es un oscilador armónico
simple cuya frecuencia angular es ω =
(K ⁄ M)1 ⁄ 2.
La masa tiene una velocidad inicial v =
(2 g0 h)1 ⁄ 2,
que es la que imprime la aceleración gravitatoria
g0 ≈
9,8 m s−2 tras una caída desde una
altura h desde el reposo. La cuerda
o muelle frena la masa según una ley sinusoidal hasta el momento en el
que se destensa. La aceleración máxima es
a = g0 [1 + (v ω ⁄ g0)2]1 ⁄ 2.
Para calcular la tensión en la cuerda y la carga de inercia que
determina la sobrepresión, hace falta sumar a esta aceleración la
aceleración gravitatoria g0.
Antes de hacer más cuentas, podemos ver que el grupo
v ω ⁄ g0
=
[E π D2 ⁄ (2 M g0]1 ⁄ 2
es independiente de la longitud de la cuerda (que es la altura
de suelta de la botella) debido a que lo que crece la rapidez por
un lado decrece la frecuencia por otro, así que al final nos sale
que tanto la tensión de la cuerda como la sobrepresión cerca del
tapón de la botella no dependen de la longitud de la cuerda.
La tensión máxima en la cuerda es
σ =
M (g0 + a) ⁄ (π D2).
Si introducimos las definiciones de arriba e igualamos esta
tensión a la resistencia de la cuerda, obtenemos una ecuación que
permite determinar el diámetro D
de la sección de cuerda, que es el único parámetro libre con el
que podemos jugar. Tras un poquito de álgebra, obtenemos este valor:
D =
{(8 ⁄ π) [(E − σu) ⁄ σu] (M g0 ⁄ σu)}1 ⁄ 2.
La resistencia es mucho más pequeña que el módulo
elástico. Podemos despreciar algún término con seguridad:
D ≈
[(8 ⁄ π) (E ⁄ σu) (m g0 ⁄ σu)]1 ⁄ 2.
Mal empezamos, pues esto toma un valor de más de 21 mm con la resistencia más baja (o unos
11 mm con la resistencia más alta).
La sobrepresión en el tapón es la que calculamos en el último artículo:
Δp =
ρ (g0 + a) l,
con una densidad del líquido ρ y una
altura de la columna de líquido l. Si sustituimos
los resultados anteriores, nos sale que la sobrepresión adopta, como mínimo
(cuando el diámetro es el mínimo admisible para evitar que la cuerda se rompa),
el siguiente valor:
Δp
= ρ g0 h [4 E (E − σu) ⁄ (σu)2 + 1]1 ⁄ 2.
Como la resistencia es mucho más pequeña que el módulo elástico, podemos
despreciar muchos términos; la siguiente expresión da casi el mismo resultado:
Δp ≈
ρ g0 h 2 E ⁄ σu.
Con una densidad similar a la del agua (1,0 Mg m−3) y una altura
de la columna de líquido de 25 cm,
la sobrepresión queda tan rematadamente grande (más de 210 veces los 25 kPa
buscados o quizá unas 100 si la resistencia
del material es la máxima y podemos permitirnos la sección más
pequeña) que esto no hay por donde cogerlo.
Habríamos obtenido los mismos resultados en menos tiempo sin más que anticipar que la aceleración gravitatoria es mucho menor que la aceleración de la botella debida a la tensión de la cuerda. Al fin y al cabo, buscábamos una aceleración de unas cien veces la gravitatoria.
Los resultados que hemos obtenido son completamente inadecuados. O cambiamos de material, o buscamos una solución más flexible. Haremos lo último en el próximo artículo.
Otros artículos de la serie
- Introducción.
- Resistencia de la pared.
- Estabilidad de un tapón de corcho.
- Planteamiento general de un experimento para medir la capacidad del tapón.
- Experimento para medir la capacidad del tapón: caso de frenada instantánea.
- Experimento para medir la capacidad del tapón: caso de frenada gradual.
- Diseño prometedor del dispositivo experimental.
Categorías: Física
Permalink: http://sgcg.es/articulos/2013/07/30/la-botella-y-la-bodega-de-avion-7/
La botella y la bodega de avión (6)
2013-07-28
Continuamos con los artículos sobre lo que pasaría con una botella cerrada y llena de algún líquido al transportarla en la bodega de un avión. Vimos que el principal problema es aguantar el salto de presión entre el ambiente de la bodega (inferior a la que hay en tierra porque la presurización es limitada) y la del interior de la botella (similar a la que había al cerrarla en tierra). Esta diferencia de presión puede estar en el entorno de los 25 kPa.
Estamos diseñando un experimento para emular el efecto de la diferencia de presión en vuelo sobre el tapón de la botella. El experimento consiste en frenar repentinamente la botella para que su contenido se agolpe contra el tapón. Antes de plantear el experimento, tenemos que estimar la cuantía de la sobrepresión alcanzada en función de las condiciones de frenado. Ayer vimos el caso límite de frenada instantánea; hoy estudiamos el caso límite de frenada gradual, lenta.
Frenada gradual
Ahora asumamos que la frenada es gradual, tal que la acústica tiene poca importancia. Si tardamos varias centésimas de segundo en detener la botella, por ejemplo, da tiempo a que las ondas acústicas viajen de un lado a otro incluso cientos de veces en una botella de dos litros típica.
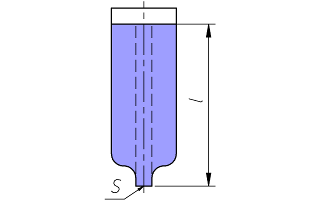
Concepto de la columna de líquido encima del tapón de la
botella invertida.
Al frenar, el tapón tiene que aguantar la masa de
la columna líquida que tiene encima. La altura de esta columna
líquida es l ≈ 25 cm
en la típica botella de dos litros. Con una densidad
ρ y una superficie del
tapón S, la masa es ρ S l. La fuerza que
hay que aguantar es el producto de esta masa por la aceleración a más la aceleración gravitatoria g0, ρ S l (a + g0),
mientras que la sobrepresión Δp
sale de dividir esta fuerza entre la superficie S de aplicación. La superficie aparecía
multiplicando y la presión sale de dividir por ella, así que al
final la superficie del tapón no es relevante para este cálculo.
Tampoco lo era en el de frenada instantánea. La sobrepresión
es
Δp =
ρ l (a + g0).
No es más que la presión
hidrostática para la carga de inercia. Con un líquido
similar al agua (cuya densidad es ρ
= 1,0 Mg m−3) y una altura
de la columna de líquido l =
25 cm, entonces basta una aceleración a + g0 =
100 m s−2 para alcanzar la
sobrepresión de 25 kPa que buscamos
modelar. Con una masa total de la botella con líquido de unos 2 kg, hace falta aplicar una fuerza de unos
200 N (equivalente a levantar cerca
de 20 kg), algo que un adulto sin
problemas de salud puede aplicar con las manos.
Otros artículos de la serie
- Introducción.
- Resistencia de la pared.
- Estabilidad de un tapón de corcho.
- Planteamiento general de un experimento para medir la capacidad del tapón.
- Experimento para medir la capacidad del tapón: caso de frenada instantánea.
- Primer diseño del experimento.
- Diseño prometedor del dispositivo experimental.
Categorías: Física
Permalink: http://sgcg.es/articulos/2013/07/28/la-botella-y-la-bodega-de-avion-6/
La botella y la bodega de avión (5)
2013-07-27
Continuamos con los artículos sobre lo que pasaría con una botella cerrada y llena de algún líquido al transportarla en la bodega de un avión. Vimos que el principal problema es aguantar el salto de presión entre el ambiente de la bodega (inferior a la que hay en tierra porque la presurización es limitada) y la del interior de la botella (similar a la que había al cerrarla en tierra). Esta diferencia de presión puede estar en el entorno de los 25 kPa.
Estamos diseñando un experimento para emular el efecto de la diferencia de presión en vuelo sobre el tapón de la botella. El experimento consiste en frenar repentinamente la botella para que su contenido se agolpe contra el tapón. Antes de plantear el experimento, tenemos que estimar la cuantía de la sobrepresión alcanzada en función de las condiciones de frenado. Empezamos estudiando el caso límite en el que detenemos la botella en un tiempo nulo.
Frenada instantánea
Asumamos en primer lugar que la botella es perfectamente rígida.
Entra en juego la acústica del contenido
líquido, que no es exactamente incompresible. Si el tapón aguanta
sin que se produzcan fugas, el líquido se frena repentinamente y esto
provoca una sobrepresión, lo que se conoce como un golpe de ariete.
La magnitud de esta sobrepresión está relacionada con la rapidez
v que tenía la botella justo
antes de frenarse y es fácil de modelar. Las perturbaciones en el
líquido se transmiten mediante ondas sonoras que viajan con velocidad
c. Digamos que todo transcurre
en un cilindro de sección S,
el cuello de la botella. En el instante de la frenada, se crea
una onda de compresión que se aleja del tapón. Un tiempo t después (tan corto que no se nota la
gravedad acelerando el fluido), la onda se ha movido una distancia
c t. Dentro del volumen
comprendido entre el tapón y el frente de onda, ha ido entrando
fluido con velocidad v y densidad
ρ (todavía sin perturbar
porque la onda no alcanza la frontera hasta el mismo instante t), de modo que tenemos una masa adicional
ρ v t.
Esta masa adicional se reparte en el volumen de longitud
c t y sección
S que ha barrido la onda,
es decir, la densidad se incrementa en una cantidad ρ v ⁄ c.
Los cambios de densidad están relacionados con los cambios de presión
mediante el módulo de compresibilidad K:
Δp =
K Δρ ⁄ ρ.
En nuestro caso, la sobrepresión es
Δp =
K v ⁄ c.
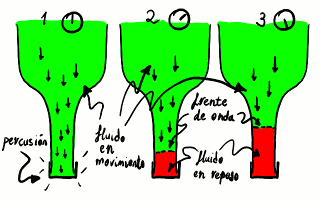
Propagación de una onda de presión en un cuello de botella
vista en tres instantes consecutivos (de izquierda a derecha).
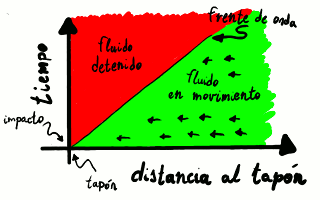
Diagrama de propagación de la onda. El eje de ordenadas es el
tiempo desde la frenada o impacto y el eje de abscisas es la distancia
al tapón que impide repentinamente el avance del fluido. Antes de ser
alcanzado por el frente de onda, el fluido no tiene noticia de la
presencia del tapón y sigue moviéndose.
Si el contenido no es muy diferente al agua, la velocidad del sonido c es próxima a 1,5 km s−1 y la compresibilidad K se parece mucho a 2,2 GPa. Haría falta una rapidez antes de la frenada muy pequeña, v = 17 mm s−1, para alcanzar el salto de presión de 25 kPa que queremos modelar. Este resultado hay que cogerlo con pinzas, por supuesto. Las hipótesis de frenada instantánea y botella perfectamente rígida son poco fieles a lo que pasa en el mundo, no obstante, así que este resultado no es más que una indicación de lo que podría alcanzarse mediante mecanismos sencillos y sin explotar la dinámica de la pared de la botella, que es flexible. Uno de los aspectos más fáciles de estudiar de la flexibilidad de la pared es una reducción de la rapidez con la que se propagan longitudinalmente las ondas debido a que la pared se estira al producirse la sobrepresión, con lo que aumenta la sección y el líquido se ajusta al nuevo espacio disponible.
La rigidez de la pared de la botella está caracterizada por el módulo elástico D del material, el diámetro D de la sección transversal y el espesor t de la pared. Sin deducirlo hoy, señalamos que la rapidez con la que se propagan las ondas largas se ve modificada de esta manera: pasa del valor c original de la velocidad del sonido en el líquido al valor modificado c ⋅ [1 + (K ⁄ E) (D ⁄ t)]−1 ⁄ 2. Una botella de vidrio (material de rigidez E = 68 GPa con un cuello cuya sección tiene un diámetro D = 25 mm y un espesor t = 5 mm ve bajada la rapidez de transmisión de ondas a unos 1,4 km s−1. En una botella de PET de pared delgada, las ondas se transmitirían más despacio, a unos pocos cientos de metros por segundo.
La formulación que usamos vale únicamente para ondas infinitesimales, con lo que modelar con esta hipótesis el efecto de la detención instantánea de la botella es como mínimo sospechoso de ser inadecuado. Esto es especialmente cierto en el caso de una botella muy flexible como una de PET de pared delgada. Incluso si se cumple la hipótesis de ondas infinitesimales, hace falta que el tiempo de frenado sea muy, muy corto. Si las ondas viajan a 1500 m s−2 y la distancia a recorrer en el seno líquido es de 25 cm (típica de una botella de dos litros), entonces las ondas van y vuelven en un tercio de milésima de segundo; la detención habría de tener lugar en un tiempo mucho más corto, de algunos microsegundos, para que fuera efectivamente instantánea.
Otros artículos de la serie
- Introducción.
- Resistencia de la pared.
- Estabilidad de un tapón de corcho.
- Planteamiento general de un experimento para medir la capacidad del tapón.
- Experimento para medir la capacidad del tapón: caso de frenada gradual.
- Primer diseño del experimento.
- Diseño prometedor del dispositivo experimental.
Categorías: Física
Permalink: http://sgcg.es/articulos/2013/07/27/la-botella-y-la-bodega-de-avion-5/
La botella y la bodega de avión (4)
2013-07-24
Continuamos con los artículos sobre lo que pasaría con una botella cerrada y llena de algún líquido al transportarla en la bodega de un avión. Vimos que el principal problema es aguantar el salto de presión entre el ambiente de la bodega (inferior a la que hay en tierra porque la presurización es limitada) y la del interior de la botella (similar a la que había al cerrarla en tierra). Esta diferencia de presión puede estar en el entorno de los 25 kPa.
Ya estudiamos lo que sucede con un tapón de corcho en una botella de vidrio. Ahora podemos preguntarnos si un un tapón de rosca, quizá acompañado de un sello, podría resistir la diferencia de presión. Aquí hay mucha variedad, tanto en materiales para la pared de la botella como, para el tapón, así como geometrías para la rosca (cómo se ajustan los perfiles del tapón y la botella). La estanqueidad del cierre es algo difícil de prever si no disponemos de información detallada que es difícil de medir. Probablemente, lo mejor que podemos hacer es un pequeño experimento en el que provocamos la sobrepresión deseada y verificamos que no hay fugas para poder afirmar con seguridad que el cierre cumplirá su objetivo dentro de la bodega del avión en vuelo.
Caso a estudiar
Para fijar ideas, vamos a trabajar sobre la hipótesis de que tenemos una botella de 2 dm3 de capacidad llena de agua. La densidad del agua es de unos 1,0 Mg m−3, así que la masa de la botella llena supera los 2,0 kg. Si el cuerpo de la botella es más o menos cilíndrico circular de unos 10 cm de diámetro, el agua ocupa una altura de unos 25 cm. Si invertimos la botella, la columna de agua es más alta debido al estrechamiento del cuello, pero supondremos que se mantiene todavía en el entorno de los 25 cm. En cuanto a la sobrepresión a modelar, buscamos unos 25 kPa, que son lo que habría de esperar de diferencia entre la presión al cerrar la botella en tierra y la presión en la bodega con el avión en la tropopausa.
El experimento
Si invertimos la botella para que quede con el tapón por debajo, la dejamos caer y la frenamos más o menos rápidamente, podemos provocar una sobrepresión que sea equivalente o superior a la que hay en vuelo. Si la botella es pequeña y manejable, a lo mejor basta con agitarla con las manos. Si no, podemos montar un arnés y agarrarla con una cuerda a un anclaje rígido para después dejarla caer. Este segundo método tiene como ventaja que es posible controlar la aceleración de frenada con cierta precisión difícil de alcanzar a mano. En función de los materiales disponibles, es posible que el montaje con la cuerda con un anclaje rígido provoque sobrepresiones excesivas y haya que buscar una solución más flexible.

Montaje experimental para provocar una sobrepresión.
En los próximos artículos realizaremos un pequeño análisis que permitirá diseñar el experimento.
Otros artículos de la serie
- Introducción.
- Resistencia de la pared.
- Estabilidad de un tapón de corcho.
- Experimento para medir la capacidad del tapón: caso de frenada instantánea.
- Experimento para medir la capacidad del tapón: caso de frenada gradual.
- Primer diseño del experimento.
- Diseño prometedor del dispositivo experimental.
Categorías: Física
Permalink: http://sgcg.es/articulos/2013/07/24/la-botella-y-la-bodega-de-avion-4/
La botella y la bodega de avión (3)
2013-07-20
Continuamos con los artículos sobre lo que pasaría con una botella cerrada y llena de algún líquido al transportarla en la bodega de un avión. Vimos que el principal problema es aguantar el salto de presión entre el ambiente de la bodega (inferior a la que hay en tierra porque la presurización es limitada) y la del interior de la botella (similar a la que había al cerrarla en tierra). Esta diferencia de presión puede estar en el entorno de los 25 kPa.
Hoy vamos a suponer que tenemos una botella de vidrio con un tapón de corcho. La botella aguanta sin problemas la diferencia de presión, pero podría suceder que la fricción contra la pared de vidrio no fuera suficiente para mantener en su sitio el tapón.
Aguante de un tapón de corcho
Vamos a hacer un cálculo rápido para estimar la máxima diferencia de presión que puede aguantar la fricción del tapón de corcho contra la pared interior de la botella antes de salir disparado. Este cálculo tiene unas inconsistencias internas que, afortunadamente, son pequeñas y hacen que el error cometido no sea muy grande.
En primer lugar, debemos tomar un modelo geométrico. Asumimos que la botella, que es perfrectamente rígida en comparación con el corcho, tiene una pared en forma de cilindro circular allí donde está el tapón. El propio tapón también es cilíndrico circular y es coaxial con la botella.
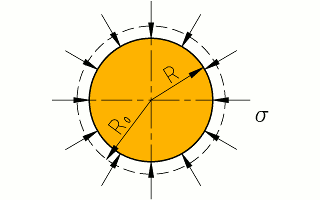
Compresión radial del tapón.
El tapón está metido a presión para que haga fuerza contra la pared
de la botella y así pueda tener buena fricción. Originalmente, el tapón
tenía un radio R0, pero
ahora está embutido con un radio R.
El corcho tiene un módulo elástico E
≈ 11 MPa; este módulo elástico relaciona la deformación
radial (el cambio relativo del tamaño del radio) y la presión σ con la que el tapón aprieta contra
la pared mediante esta expresión:
σ =
E (R0 − R) ⁄ R0.
El criterio de signos está escogido para que el valor sea positivo
cuando el tapón está apretado contra la pared, es decir, cuando
trabaja a compresión; lo habitual es asignar el signo negativo a la
compresión, no obstante. Por lo demás, el resultado sale de suponer
algunas cosillas que no son del todo descabelladas porque no queremos
afinar mucho: deformaciones infinitesimales; comportamiento elástico
lineal e isótropo; y un estado perfectamente axilsimétrico y plano.
Ya hemos aproximado la presión ejercida contra la pared,
σ. Si empujamos el tapón
a lo largo del cuello de la botella, aparece una fricción en la
superficie de contacto del corcho con el vidrio. Si hacemos poca
fuerza, el corcho se queda en su sitio. Conforme aumentamos la
fuerza, la fricción va creciendo hasta alcanzar un valor máximo;
tras alcanzar la fuerza correspondiente, la fricción deja de crecer
significativamente y el tapón desliza. La máxima tensión de
fricción τmáx
está relacionada con la presión ejercida contra la pared σ mediante un coeficiente de fricción
μ que, para la interfaz del vidrio
y el corcho, es más o menos igual a 0,5.
Con esto, la máxima tensión cortante de fricción es
τmáx =
μ σ.
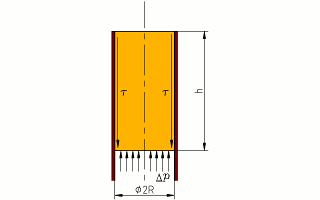
Equilibrio del tapón mediante fricción.
Ahora vamos a ver la tensión tangencial de fricción que
sería necesaria para retener el tapón en su sitio. Con una
diferencia de presión Δp
entre el exterior y el interior de la botella, la fricción
promedio τ es la que sale
de repartir por la cara en contacto con la pared (un cilindro de
altura h y circunferencia 2 π R) la resultante de aplicar
el salto de presión en el área de la base del tapón (un círculo
de área π R2):
τ
= Δp R ⁄ (2 h).
Esta tensión es positiva cuando se opone al salto de presión.
Supondremos que la presión en toda la pared es aproximadamente igual
al promedio, lo nos hace las cuentas muy fáciles.
Juntemos todo. Para que el tapón aguante en su sitio, la fricción
ha de estar por debajo del valor máximo:
τ < τmáx.
Con las expresiones derivadas anteriormente, esto queda así:
Δp R ⁄ (2 h)
<
μ E (R0 − R) ⁄ R0.
¡Un tapón de altura h = 4 cm
cuyo radio original fuera R0 = 1,05 cm
y cuyo radio embutido fuera R = 1 cm podría aguantar
un salto de presión de hasta 2,1 MPa!
Esto es mucho más grande que los 25 kPa
que podemos esperar. Un tapón real, con irregularidades y defectos,
aguantaría menos.
Otros artículos de la serie
- Introducción.
- Resistencia de la pared.
- Planteamiento general de un experimento para medir la capacidad del tapón.
- Experimento para medir la capacidad del tapón: caso de frenada instantánea.
- Experimento para medir la capacidad del tapón: caso de frenada gradual.
- Primer diseño del experimento.
- Diseño prometedor del dispositivo experimental.
Categorías: Física
Permalink: http://sgcg.es/articulos/2013/07/20/la-botella-y-la-bodega-de-avion-3/
La botella y la bodega de avión (2)
2013-07-17
Introdujimos recientemente el problema de la supervivencia de una botella cerrada y llena de algún líquido en la bodega de un avión en vuelo. Vimos que aunque el avión está presurizado, la presión desciende un poco a gran altitud: puede bajar hasta unos 75 kPa, alrededor de 25 kPa menos que a nivel del mar y 20 kPa menos que en Madrid lejos de las montañas. Con la botella sellada, la presión interior no cambia significativamente porque la temperatura de la bodega no varía mucho, así que hay un exceso de presión Δp en el interior de la botella de esos 25 kPa si fue cerrada a nivel del mar. Este exceso de presión ha de estar dentro del rango que puede aguantar la botella sin perder su integridad.
Resistencia de la pared de la botella
Asumamos en primer lugar que el tapón aguanta en su sitio y mantiene la botella bien cerrada. Si es así, tendremos que ver si la propia botella es capaz de aguantar el esfuerzo debido a la diferencia de presión. La botella en sí es una estructura de pared delgada y podemos hacer algunas hipótesis simplificadoras que nos facilitan mucho los cálculos: las tensiones son muy aproximadamente uniformes según el espesor de la pared y la componente contenida en la superficie media de la pared es mucho mayor que cualquier otra. La siguiente figura ilustra lo que pasa con las tensiones circunferenciales:
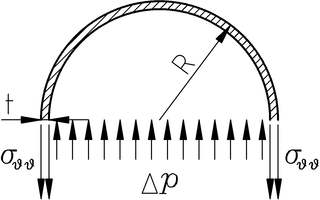
Tensión circunferencial en la botella. Esta tensión es mucho
mayor que la tensión radial (que es como el salto de presión).
Asumimos que la botella es aproximadamente cilíndrica circular.
Esto es al menos cierto hasta llegar al estrechamiento del cuello.
El radio de la botella es R
y el espesor es t.
De esta manera, la tensión circunferencial σθθ
ha de equilibrar en dos veces el espesor (2 t)
el salto de presión Δp en
todo el diámetro (2 R):
σθθ ⋅ 2 t
= Δp ⋅ 2 R,
es decir,
σθθ
= Δp ⋅ (R ⁄ t).
Como la relación R ⁄ t
es grande, la tensión circunferencial σθθ
es mucho mayor que el mero salto de presión Δp. En la bodega de
avión, el salto de presión puede ser perfectamente Δp = 25 kPa; una botella de PET
con un diámetro 2 R = 6 cm
y una pared delgadita de espesor t =
0,25 mm tendría que suportar tensiones circunferenciales
σθθ =
3 MPa, pero el PET puede aguantar cómodamente varias
decenas de megapascales, así que la botella está segura.
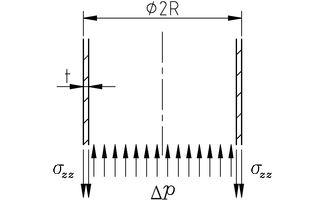
Tensión axial en la botella.
Las tensiones axiales σzz
salen de un cálculo similar al de las tensiones circunferenciales.
La tensión axial repartida en la circunferencia y en el espesor, σzz ⋅ 2 π R t
compensa la presión en la base Δp ⋅ π R2.
La tensión axial es, por lo tanto,
σzz
= Δp ⋅ R ⁄ (2 t).
Esto es la mitad de lo que salió para la tensión circunferencial.
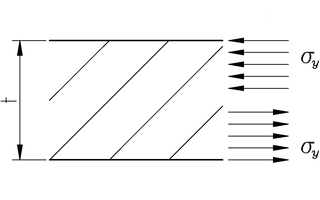
Tensiones debidas a la flexión en la base de la botella. En el
límite elástico, cuando el espesor está completamente agotado,
tomamos como modelo que la mitad del espesor trabaja a compresión
y la otra mitad trabaja a tracción, en ambas mitades con tensión
igual en valor absoluto al límite elástico. Con cargas mayores,
el material se deforma plásticamente en gran magnitud y con poco
esfuerzo y colapsa tras aumentar poco la carga.
Todavía quedan tensiones importantes. La base es más o menos una placa que opera a flexión. Trabajar a flexión significa compensar momentos con tensiones dentro del plano de la placa; en la figura anterior, un momento que obliga a flectar hacia abajo provoca tracción en la parte superior del espesor y compresión en la parte inferior. La teoría elemental de placas (que queda fuera del alcance de este artículo) indica como buena estimación del momento flector por unidad de longitud más grande (que aparece donde la base se encuentra con el lateral) es Δp R2 ⁄ 8. Si asumimos que el material aguanta hasta que se aguanta todo el espesor, de modo que la mitad del espesor está en tracción a la máxima tensión admisible (el límite elástico) y la otra mitad está en compresión también a la máxima tensión admisible, equilibrar el momento flector obliga a que esta tensión sea Δp R2 ⁄ (2 t2). El espesor de 0,25 mm daría una tensión muy falsa, 180 MPa; el PET aguanta unos 55 MPa (quizá más) antes de plastificar, así que necesitamos un espesor como de medio milímetro o más grande en la base y la zona de la pared lateral próxima a la base.
Otros artículos de la serie
- Introducción.
- Estabilidad de un tapón de corcho.
- Planteamiento general de un experimento para medir la capacidad del tapón.
- Experimento para medir la capacidad del tapón: caso de frenada instantánea.
- Experimento para medir la capacidad del tapón: caso de frenada gradual.
- Primer diseño del experimento.
- Diseño prometedor del dispositivo experimental.
Categorías: Física
Permalink: http://sgcg.es/articulos/2013/07/17/la-botella-y-la-bodega-de-avion-2/
Recogida de firmas para pedir que se evite la ruina del CSIC
2013-07-11
El Consejo Superior de Investigaciones Científicas está al borde del colapso económico. Los recortes en la financiación de los últimos años han conducido han llevado a un déficit de 150 millones de euros que, con ajustes internos, se reduce a 100 millones de euros. el Estado va a aportar 75 millones de euros, sin duda bajo el enfoque de que insuficiente es mejor que nada. La cosa está mal, así que hay una recogida de firmas que busca hacer presión para que el Estado cumpla con su deber de garantizar el funcionamiento de su principal institución científica. Estas recogidas de firmas, por supuesto, tienen escasa o nula validez jurídica, pero tienen cierto atractivo como indicadores de la opinión de parte de la población.
Categorías: Actualidad
Permalink: http://sgcg.es/articulos/2013/07/11/recogida-de-firmas-para-pedir-que-se-evite-la-ruina-del-csic/
La botella y la bodega de avión (1)
2013-07-09
Recientemente, me preguntaron sobre el probable destino de cierta botella y su líquido contenido al viajar en la bodega de un avión. ¿Podría explotar? ¿Podría tener una fuga? Esto depende de la botella en cuestión, su contenido y su cierre. Vamos a ver en varios capítulos lo que pasa; hoy toca el origen de todos nuestros problemas: el salto de presión.
Saltos de presión
La presión tiene mucho que decir en este asunto. La botella se cerró en tierra y, desde entonces, quedó sellada. Dentro de cierto rango de temperaturas y presiones, la botella se deforma muy poco y, al no haber fugas, la presión del interior se mantiene más o menos constante. Por supuesto, incluso si la botella es indeformable, la presión del interior puede variar un poco al hacerlo la temperatura ambiente. La botella contiene tanto líquido como aire gaseoso; con un contenido líquido bien incompresible sin gas saturado y una botella que no se deforma, el volumen de gas no varía y, como el aire es muy parecido a un gas ideal (salvo en condiciones extremas), la temperatura y la presión varían proporcionalmente. Si la temperatura varía poco (digamos un descenso de 20 K frente al entorno de los 300 K de una vivienda), entonces la presión también cambia en la misma proporción: una botella cerrada en Madrid a 94 kPa quedaría a 88 kPa tras un descenso de unos 20 K al meterla en un frigorífico.
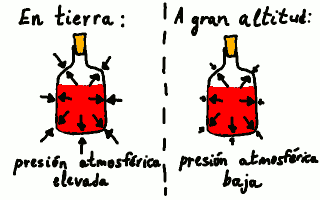
Presión en el interior de una botella comparada con la atmosférica.
Las flechas negras representan cualitativamente la magnitud de la presión:
las flechas grandes indican presión alta y las flechas pequeñas indican
presión baja. La botella se mantiene más o menos a la presión que tenía
al cerrarla en tierra si la temperatura no varía significativamente.
La presión atmosférica cambia con la altitud. Podemos estimarla con un modelo como el de la atmósfera estándar. Ahora bien, la botella no está suelta y flotando en medio del aire: está guardada en el interior de la bodega de un avión. En un reactor comercial típico, la bodega está presurizada de modo que la presión en su interior no queda por debajo de la correspondiente a una altitud de 2400 m en atmósfera estándar: unos 75 kPa. En cuanto a la temperatura, ésta es variable, pero podemos asumir que no desciende en exceso, aunque puede ser un poquito más fría que la de la cabina de pasajeros. En tales condiciones, una botella indeformable y bien sellada mantendría su contenido a una presión superior similar a la de tierra y superior a la del ambiente en vuelo.
Otros artículos de la serie
- Sobre la resistencia de la pared de la botella.
- Estabilidad de un tapón de corcho.
- Planteamiento general de un experimento para medir la capacidad del tapón.
- Experimento para medir la capacidad del tapón: caso de frenada instantánea.
- Experimento para medir la capacidad del tapón: caso de frenada gradual.
- Primer diseño del experimento.
- Diseño prometedor del dispositivo experimental.
Categorías: Física
Permalink: http://sgcg.es/articulos/2013/07/09/la-botella-y-la-bodega-de-avion-1/
Un velocímetro y un cuentakilómetros son dos cosas distintas
2013-07-05
SGCG ofrece este mensaje educativo de utilidad pública: un velocímetro y un cuentakilómetros son dos cosas diferentes. El velocímetro indica la rapidez del desplazamiento de un vehículo, mientras que el cuentakilómetros da la distancia recorrida. No es difícil de distinguir y, presumiblemente, casi cualquier adulto capaz de conducir un vehículo automóvil tiene capacidad de sobra para diferenciar qué es cada cosa.
Categorías: Lingüística
Permalink: http://sgcg.es/articulos/2013/07/05/un-velocimetro-y-un-cuentakilometros-son-dos-cosas-distintas/
Día Internacional del Moonwalk
2013-07-01
Recordamos que el 1 de julio es el Día Internacional del Moonwalk, el día dedicado al paso de baile que consiste en deslizarse de modo que se da la impresión de que se camina en sentido contrario al del propio movimiento. Si hay un buen momento para marcarse un buen moonwalk, ese momento es ahora.
Permalink: http://sgcg.es/articulos/2013/07/01/dia-internacional-del-moonwalk/
