Marzo de 2016
Calendario de artículos de de 2016
| lu | ma | mi | ju | vi | sá | do |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 | |||
Campeonato del Mundo de Patinaje Artístico sobre Hielo de 2016 (2)
2016-03-31
Esta semana se celebra el Campeonato del Mundo de Patinaje Artístico sobre Hielo de 2016 en Boston. Compiten por España Javier Fernández (actual campeón del mundo) y Javier Raya en la categoría individual masculina; Sonia Lafuente en la categoría individual femenina; y Celia Robledo y Luis Fenero en danza.
Ayer tocaron los cortos de danza y de la categoría individual masculina.
- En danza, Celia Robledo y Luis Fenero no pudieron superar el corte para llegar a la final. En el primer puesto tenemos a unos espectaculares Gabriella Papadakis y Guillaume Cizeron que están que pueden con todo. No muy lejos se encuentran Maia Shibutani y Alex Shibutani, también muy fuertes. El tercer puesto está en manos de Madison Chock y Evan Bates, pero Kaitlyn Weaver y Andrew Poje pueden tener algo que decir.
- En la categoría individual masculina, Javier Raya ha estado a punto de alcanzar el corte para la final, pero no lo ha logrado. Javier Fernández, con el cuádruple salchow atravesado, va segundo, pero el amigo Yuzuru Hanyu ha vuelto a rozar la perfección absoluta y saca una ventaja enorme. En tercer puesto está Patrick Chan.
Hoy tocan los cortos femeninos y los largos de danza.
Categorías: Actualidad, Deporte
Campeonato del Mundo de Patinaje Artístico sobre Hielo de 2016 (1)
2016-03-30
Esta semana se celebra el Campeonato del Mundo de Patinaje Artístico sobre Hielo de 2016 en Boston. Compiten por España Javier Fernández (actual campeón del mundo) y Javier Raya en la categoría individual masculina; Sonia Lafuente en la categoría individual femenina; y Celia Robledo y Luis Fenero en danza.
Hoy tocan los cortos de danza y de la categoría individual masculina.
Categorías: Actualidad, Deporte
Teorema de Bayes
2016-03-27
El teorema de Bayes es un resultado de la teoría de la probabilidad que es sencillo pero muy útil. Sirve para relacionar la probabilidad condicionada en un sentido con la probabilidad condicionada en sentido opuesto.
Tomemos dos fenómenos A y B y hagamos uso de la relación entre la probabilidad conjunta y la probabilidad condicionada. La probabilidad del fenómeno A condicionada a la verificación del fenómeno B es
P(A|B) = P(A∩B) ⁄ P(B).
La probabilidad del fenómeno B condicionada a la verificación del fenómeno A es
P(B|A) = P(B∩A) ⁄ P(A).
Ahora bien, la probabilidad conjunta es la misma si se toma en un sentido en otro, ya que la conjunción conmuta:
P(A∩B) = P(B∩A).
Por lo tanto, tenemos la siguiente relación:
P(A|B) P(B) = P(A∩B) = P(B∩A) = P(B|A) P(A).
Otra manera de escribir la anterior relación es como sigue:
P(A|B) = P(B|A) P(A) ⁄ P(B).
La expresión anterior es el teorema de Bayes y es una herramienta que se usa constantemente en estadística, ya que permite conocer la probabilidad condicionada en un sentido cuando se conoce la probabilidad condicionada en el sentido opuesto.
Categorías: Matemáticas
Permalink: http://sgcg.es/articulos/2016/03/27/teorema-de-bayes/
Probabilidad conjunta frente a la probabilidad condicionada (2)
2016-03-26
Ayer vimos la sutil o no tan sutil diferencia entre la probabilidad conjunta y la probabilidad condicionada. Ahora vamos a estudiar cómo podemos definir una si conocemos la otra.
Paso de la probabilidad conjunta a la probabilidad condicionada
Si tenemos dos fenómenos A y B y conocemos la probabilidad conjunta P(A∩B) (que es la probabilidad de que se den simultáneamente los fenómenos A y B tomando como referencia todo el espacio de posibilidades), la probabilidad condicionada P(A|B) queda determinada sin más que referir la probabilidad de que se produzcan ambos fenómenos no al espacio de posibilidades completo, sino el restringido a que se produzca el fenómeno B:
P(A|B) = P(A∩B) ⁄ P(B).
Como la probabilidad está comprendida entre 0 y 1, la probabilidad condicionada es mayor o igual que la probabilidad conjunta.
Como ejemplo de aplicación, digamos que el mes de marzo (que tiene 31 días) llueve durante 7 días, de manera que si escogemos un día cualquiera del año, la probabilidad de que sea un día lluvioso de marzo corresponde a
P(llueve∩marzo) = 7 ⁄ 365.
Se trata de una probabilidad conjunta. Por simplificar, hemos asumido que el año tiene 365 días exactamente. La probabilidad de que un día cualquiera caiga en el mes de marzo es
P(marzo) = 31 ⁄ 365.
La probabilidad condicionada P(llueve|marzo), que es la probabilidad de que un día llueva si se sabe que ese día cae en el mes de marzo, es
P(llueve|marzo) = P(llueve∩marzo) ⁄ P(marzo) = (7 ⁄ 365) ⁄ (31 ⁄ 365) = 7 ⁄ 31.
Esta probabilidad condicionada es mayor que la probabilidad conjunta.
Paso de la probabilidad condicionada a la probabilidad conjunta
De forma inversa, si conocemos la probabilidad conjunta P(A|B) (que es la probabilidad de que se den simultáneamente los fenómenos A y B tomando como referencia solamente los casos en los que se da el fenómeno B), la probabilidad conjunta P(A∩B) queda determinada sin más que referir la probabilidad condicionada al espacio de posibilidades completo:
P(A∩B) = P(A|B) P(B).
Como las probabilidades están comprendidas entre 0 y 1, la probabilidad conjunta es menor o igual que la probabilidad condicionada.
Como ejemplo de aplicación, digamos que el mes de marzo (que tiene 31 días llueve durante 7 días, de manera que si escogemos un día cualquiera del mes de marzo, la probabilidad de que sea un día lluvioso corresponde a
P(llueve|marzo) = 7 ⁄ 31.
Se trata de una probabilidad condicionada. La probabilidad de que un día cualquiera caiga en el mes de marzo es
P(marzo) = 31 ⁄ 365.
Por simplificar, hemos asumido que el año tiene 365 días exactamente. La probabilidad conjunta P(llueve∩marzo), que es la probabilidad de que un día cualquiera sea un día lluvioso de marzo, es
P(llueve∩marzo) = P(llueve|marzo) P(marzo) = (7 ⁄ 31) (31 ⁄ 365) = 7 ⁄ 365.
Esta probabilidad conjunta es menor que la probabilidad condicionada.
Categorías: Matemáticas
Permalink: http://sgcg.es/articulos/2016/03/26/probabilidad-conjunta-frente-a-probabilidad-condicionada-2/
Probabilidad conjunta frente a probabilidad condicionada
2016-03-25
Hemos presentado dos herramientas matemáticas que sirven para el estudio de la probabilidad de dos o más sucesos: la probabilidad conjunta y la probabilidad condicionada. Es fácil confundir una con la otra debido a que describen conceptos similares. Si tenemos dos fenómenos A y B, tanto la probabilidad conjunta como la probabilidad condicionada describen la probabilidad de que se den ambos fenómenos, pero dicha probabilidad está referida a espacios de posibilidades diferentes:
- La probabilidad conjunta P(A∩B) es la probabilidad de que se produzcan simultáneamente los fenómenos A y B dentro del espacio de posibilidades total.
- La probabilidad condicionada P(A|B) es la probabilidad de que se produzca el fenómeno A dentro del espacio de posibilidades restringido en el que se verifica el fenómeno B.
Una manera de ver la diferencia es a través de unos diagramas de Venn. En primer lugar, veamos el diagrama general, en el que aparecen el espacio de posibilidades completo U (el conjunto de todas las posibilidades), el conjunto en el que se produce el fenómeno A y el conjunto en el que se produce el fenómeno B:
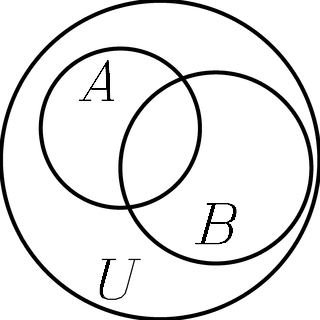
Conjuntos del espacio de posibilidades. Cada conjunto es el área
de un círculo. Los conjuntos A
y B, que en este caso se superponen,
están contenidos dentro del
conjunto U de todas las
posibilidades.
La probabilidad conjunta vendría representada por el siguiente diagrama:
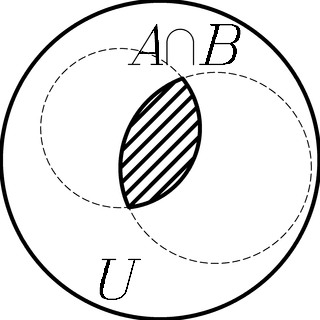
Probabilidad
conjunta P(A∩B). El
espacio de posibilidades al que está referida la probabilidad conjunta
es el total, U.
Finalmente, la probabilidad condicional vendría representada por el diagrama siguiente:
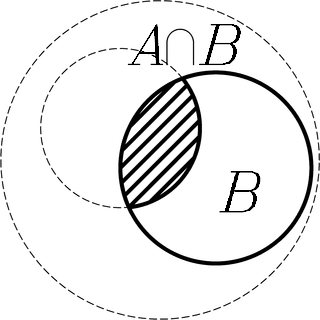
Probabilidad
condicionada P(A|B). El
espacio de posibilidades al que está referida la probabilidad
condicionada es el que verifica B.
Tomemos como ejemplo que con la notación anterior, A es que un día dado llueve y B es que un día dado cae en pleno mes de marzo. La probabilidad conjunta P(A∩B) podría interpretarse desde un punto de vista frecuentista como el cociente del número de días que llueve y es el mes de marzo entre el número de días que tiene el año, mientras que la probabilidad condicionada P(A|B) quedaría interpretada como el cociente del número de días lluviosos del mes de marzo entre el número de días que tiene el propio mes de marzo.
Categorías: Matemáticas
Permalink: http://sgcg.es/articulos/2016/03/25/probabilidad-conjunta-frente-a-probabilidad-condicionada/
Probabilidad conjunta
2016-03-22
La probabilidad conjunta es la probabilidad de que sucedan varios fenómenos simultáneamente. Por ejemplo, podemos estudiar desde un punto de vista frecuentista la probabilidad conjunta de que salga cara en dos tiradas de una moneda justa: se trataría de ver en cuántos casos frente al total se dan las dos caras. Hay cuatro resultados posibles:
- cara en el primer lanzamiento y cara en el segundo lanzamiento;
- cara en el primer lanzamiento y cruz en el segundo lanzamiento;
- cruz en el primer lanzamiento y cara en el segundo lanzamiento;
- cruz en el primer lanzamiento y cruz en el segundo lanzamiento.
De estos cuatro resultados, solamente uno consiste en cara en ambos lanzamientos; por lo tanto, la probabilidad conjunta de obtener cara en el primer lanzamiento y obtener cara en el segundo lanzamiento sería igual a un cuarto.
Si nos limitamos a dos fenómenos A y B, una forma popular de escribir su probabilidad conjunta es la siguiente:
P(A∩B).
Puede pensarse que esta notación hace hincapié en una interpretación de la probabilidad como una medida del tamaño de los conjuntos de resultados dentro del espacio de posibilidades.
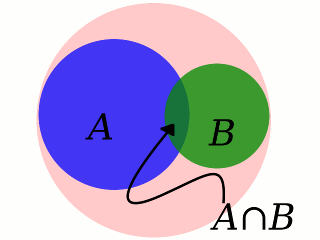
Diagrama de Venn que ilustra la probabilidad conjunta. La
probabilidad P(A) es el área del
círculo A dividida entre el área del
círculo del fondo (que representa el espacio de posibilidades); la
probabilidad P(B) es el área del
círculo B dividida entre el área del
círculo del fondo; finalmente, la probabilidad
conjunta P(A∩B) es el área
de la intersección A∩B
dividida entre el área del círculo del fondo.
La notación puede extenderse fácilmente. Por ejemplo, si tuviéramos tres fenómenos A, B y C, su probabilidad conjunta (la probabilidad de que se dieran los tres simultáneamente) podría quedar escrita como sigue:
P(A∩B∩C).
La probabilidad conjunta de un conjunto de fenómenos {A1,A2,…} podría quedar escrita así:
P(∩nAn).
Usaremos en artículos posteriores la notación expuesta hoy.
Categorías: Matemáticas
Permalink: http://sgcg.es/articulos/2016/03/22/probabilidad-conjunta/
Probabilidad condicionada
2016-03-20
Ya vimos que el concepto matemático de la probabilidad puede significar varios conceptos diferentes (pero relacionados entre sí) en el mundo físico. Hoy vamos a hablar de un caso particular de probabilidad: la probabilidad condicionada, que es la probabilidad de un fenómeno cuando nos limitamos a estudiar los casos en los que se da otro fenómeno. Si formalmente y de forma habitual escribimos la probabilidad de un suceso A así:
P(A),
la probabilidad condicionada de A dado un suceso B se escribe así habitualmente:
P(A|B).
Cuando tomamos la probabilidad de un fenómeno sin condicionar, estudiamos todo el espacio de posibilidades. Al evaluar una probabilidad condicionada, lo que hacemos es limitarnos a estudiar los casos en los que se da la condición. Por ejemplo, podemos preguntarnos cuál es la probabilidad de que llueva un día cualquiera de todo el año y eso sería una probabilidad sin condicionar:
P(llueva),
pero también podemos preguntarnos cuál es la probabilidad de que llueva un día cualquiera del mes de marzo y eso sería una probabilidad condicionada:
P(llueva|estamos en marzo).
Hablar de probabilidad condicionada es lo mismo que hablar de probabilidad cuando se restringen las condiciones en las que se desarrollan los hechos.
La siguiente figura sirve para ilustrar el concepto de la probabilidad condicionada desde un punto de vista frecuentista:
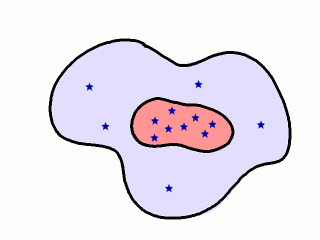
Ilustración de una interpretación frecuentista de la probabilidad
condicionada.
Estudiamos la probabilidad de encontrar una estrellita como algo proporcional al número de estrellitas que hay por unidad de superficie. La probabilidad general es proporcional al número total de estrellitas dividido entre el área grande coloreada (que incluye la superficie pequeña del interior), mientras que la probabilidad condicionada a estar en el área interior es proporcional al número de estrellitas que hay en el área interior dividido entre la superficie del área interior. Como hay más concentración de estrellitas en el área interior (que es menor que el área total), la probabilidad de encontrar una estrellita condicionada a que esté en el área interior es más grande que la probabilidad de encontrar una estrellita en general.
Desde el punto de vista bayesiano, la probabilidad condicionada es la probabilidad que asignamos a un suceso tras conocer cierta información (que se da el fenómeno condicionante). De vuelta al ejemplo de la lluvia, la probabilidad general de que llueva es la que asignamos cuando no sabemos en qué día estamos, mientras que la probabilidad de que llueva condicionada a que es el mes de marzo es la que asignamos cuando conocemos el dato de que estamos en pleno mes de marzo.
La probabilidad condicionada no es lo mismo que la probabilidad de que ocurran dos hechos simultáneamente: en el ejemplo anterior, hablamos de cómo de probable es que llueva limitándonos a estudiar los días de marzo, no cómo de probable es que llueva y sea marzo al mismo tiempo.
Categorías: Matemáticas
Permalink: http://sgcg.es/articulos/2016/03/20/probabilidad-condicionada/
Gemelos de ébano
2016-03-15
Necesitaba unos gemelos para una camisa. Tenía unas tablillas de ébano de silvicultura sostenible y decidí cortar un trocito de una para fabricar los gemelos que me hacían falta. Los gemelos son como el de la siguiente fotografía:

Gemelo sujetando una manga.
La tablilla era de 6 mm de espesor. Corté piezas circulares de unos 14 mm con una sierra de marquetería. Con cada pieza, el trabajo fue como ilustran las siguientes fotografías:

Hice casi todo el trabajo en el torno. La pieza va sujeta con
cianoacrilato a un palo redondo de haya.

La forma de la parte vista del gemelo está hecha con un raspador y
una lija gruesa.

La superficie vista está acabada con lijas de grano creciente
hasta llegar al 12000, que da como resultado un pulido brillante.
Quizá habría sido posible parar antes de alcanzar el grano 12000.

El cuello está cilindrado con una gubia delgada y un bedano.

El cuello está taladrado según la dirección radial con una broca
de 1,5 mm. A falta de un taladro de
columna, la fresadora vertical miniatura sirve perfectamente.
Tras hacer los trabajos de torneado y taladrado, separé cada pieza del palo. Con las tres primeras piezas, el cianoacrilato saltó limpiamente, pero con la última hubo que hacer un pequeño corte para facilitar la separación.

Las piezas están unidas a pares con hilo elástico anudado a través
del agujero del cuello.
Categorías: DIY
Permalink: http://sgcg.es/articulos/2016/03/15/gemelos-de-ebano/
¿Qué son las mujeres?
2016-03-13
Llegan algunas fechas como el Día Internacional de la Mujer y mucha
gente se acuerda de que las mujeres existen y difunde mensajes sobre
lo importantes que son: son nuestras madres, nuestras hermanas,
nuestras amigas…
Parece que si hay que definir a la mujer
de alguna manera, es como algo relativo al hombre, de acuerdo a la
función que desempeña para el hombre. Eso es no haber entendido nada.
¿Qué son las mujeres? Las mujeres son personas, sin más.
Exactamente igual que los hombres. De eso trata el Día Internacional
de la Mujer.
Categorías: Derechos
Permalink: http://sgcg.es/articulos/2016/03/13/que-son-las-mujeres/
La interpretación frecuentista y la interpretación bayesiana de la probabilidad
2016-03-10
La probabilidad puede describir varios conceptos diferentes, pero que se acogen a la misma descripción matemática. Dos de las interpretaciones más populares dicen que la probabilidad es:
- La frecuencia con la que se da un resultado (digamos que el de un experimento o el de un juego de azar) cuando se repite una acción (digamos el experimento o la partida al juego de azar) muchas veces. Esta interpretación hace hincapié en el hecho objetivo, empírico.
- El grado de creencia o confianza que tenemos en que el resultado se produzca. Esta interpretación hace hincapié en el hecho subjetivo.
Hay otras interpretaciones de la probabilidad más o menos formales y más o menos establecidas: por ejemplo, podemos interpretar la probabilidad como una medida de la tendencia a producirse que muestra un fenómeno.
Para aumentar la confusión, hay métodos estadísticos que son más utilizados desde un enfoque frecuentista y otros métodos estadísticos que son más utilizados desde un enfoque bayesiano. Esto lleva en ocasiones a cierto debate sobre qué enfoque es mejor, aunque es posible argumentar que ambos son complementarios, ambos dan resultados muy útiles en la práctica y, de hecho, nada impide aplicar una interpretación bayesiana a los métodos «frecuentistas» o una interpretación frecuentista a los métodos «bayesianos».
La teoría de la probabilidad es independiente de estas interpretaciones: parte de una base axiomática que define lo que es la probabilidad de acuerdo a unas propiedades que cumple. La teoría matemática que resulta de esta base axiomática describe objetos abstractos que tienen grandes aplicaciones prácticas, ya que tanto la probabilidad frecuentista como la probabilidad bayesiana (y otras «manifestaciones físicas» de la probabilidad) se comportan de acuerdo a las leyes que describen la probabilidad matemática abstracta.
Categorías: Matemáticas
La hipótesis nula en inferencia estadística
2016-03-08
Por lo general, cuando se quiere comprobar experimentalmente la validez de una hipótesis científica, se recurre a métodos estadísticos que guían a la hora de sacar conclusiones. Muchos de estos métodos estadísticos consisten en contraponer la hipótesis cuya validez se quiere comprobar y una segunda hipótesis, la hipótesis nula, que ha de ser falsa para que la primera hipótesis sea verdadera. Una hipótesis nula típica es que no existe relación entre varios fenómenos. Por ejemplo, digamos que tenemos la siguiente hipótesis que deseamos validar:
Si llueve, el suelo se moja.
Una hipótesis nula podría ser la siguiente:
Que se moje el suelo es independiente de si llueve o no.
Igual que las hipótesis de trabajo pueden ser en general muy abundantes, no hay escasez de hipótesis nulas que utilizar. Para el ejemplo anterior de la lluvia y el suelo, podríamos plantear una hipótesis nula un poquito más formal:
La humedad promedio en el suelo es la misma llueva o no llueva.
También podríamos hacer una hipótesis nula más restrictiva:
La distribución estadística de la humedad en el suelo es la misma llueva o no llueva.
Esta segunda hipótesis nula implica la primera, pero la primera no implica la segunda.
A la hora de evaluar la validez de una hipótesis científica, muy a menudo lo que se hace es evaluar la probabilidad de encontrar los resultados experimentales obtenidos si la hipótesis nula fuera cierta. Cuando esta probabilidad es baja, parece poco probable que la hipótesis nula sea cierta y podría considerarse esto como evidencia a favor de la hipótesis científica bajo evaluación. La situación, como veremos más adelante, es un poco más complicada.
Categorías: Matemáticas
Permalink: http://sgcg.es/articulos/2016/03/08/la-hipotesis-nula-en-inferencia-estadistica/
